Основы алгоритмизации

Лекция 9

План лекции:

Понятие алгоритма

Процесс решения задач на ЭВМ предполагает выполнение следующих этапов: формулировка задачи, выбор метода решения задачи, составление алгоритма, составление программы, решение задачи на ЭВМ с помощью программы.

Следовательно, основные понятия этого процесса: метод- алгоритм- программа.

Алгоритм - это метод (способ) решения задачи, записанный по определенным правилам, обеспечивающим однозначность его понимания и механического исполнения при всех значениях исходных данных (из некоторого множества значений).

В толковом словаре по «Информатике» (1991) дано общепринятое определение этого понятия:

Алгоритм - точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату.

Основные свойства алгоритма

1. Дискретность. Это свойство означает, что процесс решения задачи, определяемый алгоритмом разделен на отдельные шаги, и, естественно, алгоритм представляет собой последовательность команд.
2. Определенность алгоритма. Каждая команда алгоритма должна быть понятна исполнителю и не допускать неоднозначного толкования и неопределенного исполнения.
3. Результативность алгоритма. Состоит в том, что алгоритм всегда приводит к результату через конечное число шагов.
4. Массовость алгоритма. Означает, что каждый алгоритм, разработанный для решения какой- то задачи должен быть применим для решения задач этого типа при всех допустимых значениях исходных данных.

Способы описания алгоритмов

1. Словесно- формульное описание алгоритма (т.е описание с помощью слов и формул).

Пример: Составить алгоритм начисления зарплаты согласно следующим правилам:

Если стаж работы сотрудника менее 5 лет, то зарплата- 500 рублей; при стаже от 5 лет до 10 лет- 700 рублей; при стаже свыше 10 лет зарплата ежегодно увеличивается на 20 рублей.

{

В математическом виде задача выглядит так:

500, если ST < 5

Вычислить ZP = 700, если 5 ≤ ST ≤ 10

700 + (ST – 10) * 20, если 10 < ST

где ZP- зарплата; ST- стаж работы.

Словесно формульное описание алгоритма этой задачи выглядит так:

1. Ввести ST, перейти к п.2.
2. Если ST < 5, то ZP: = 500, перейти к п.4, иначе в п.3.
3. Если ST ≤ 10, то ZP: = 700, перейти в п.4, иначе ZP: = 700 + (ST-10) * 20 перейти в п.4.
4. Вывести (отпечатать) значение ZP, перейти в п.5.
5. Остановить вычисления.

2. Графическое описание алгоритма (т.е. описание с помощью схем).

Схема представляет собой систему связанных геометрических фигур. Каждая фигура обозначает этап решения задачи и называется блоком. Порядок выполнения операций (этапов) указывается стрелками, соединяющими блоки.

В схеме блоки стараются размещать сверху вниз, в порядке их выполнения. Операции обозначают различными фигурами:

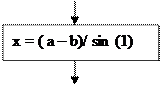§ Операция присвоения (блок «Процесс»)- используется для обозначения действий или последовательности действий.

§ Операции Ввод и Вывод

§ Операции «Условный переход» (блок «решения»). В каждом блоке «решение» должен быть указан вопрос, условие или сравнение.

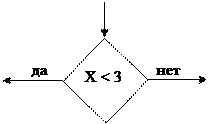§ Начало процесса решения задачи обозначается блоком

§ Завершение процесса решения задачи обозначается блоком

Пример: Схема алгоритма задачи про зарплату.

«Модификация». Используется для организации циклических конструкций.

Внутри блока указан параметр цикла, указывается его начальное значение, граничное условие и шаг изменение значения параметра для каждого повторения.

§ Предопределенный процесс используется для указания обращений к вспомогательным алгоритмам.

§ «Документ» - вывод результатов не печать.

3. Описание алгоритма на алгоритмическом языке.

Алгоритмический язык- это средство для записи алгоритма в аналитическом виде, промежутком между записью алгоритма на естественном языке и записью на языке ЭВМ (языке программирования).

Пример с зарплатой:

Используется ограниченный набор терминов и строже правила записи операций.

алг ЗАРПЛАТА (цел ST, вещ ZP)

арг ST

рез ZP

нач

если ST < 5

то ZP: = 500

иначе

если ST < = 10

то ZP: = 700

иначе ZP: = 700 + (ST - 10) * 10

все

все

кон

Вывод: Сравнение разных способов показывает, что наиболее наглядным является способ схемы алгоритмов.

Основные принципы построения алгоритмов

1. Выявить исходные данные, результаты, назначить их имена.

2. Выбрать метод (порядок) решения задачи.

3. Разбить метод решения на задачи.

4. Изобразить каждый этап в виде соответствующего блока схемы алгоритма и указать порядок их выполнения.

5. В полученной схеме при любом варианте вычислений:

§ Предусмотреть выдачу результатов или сообщений об их отсутствии;

§ Обеспечить возможность перейти после выполнения любой операции к блоку «Останов» (к выходу схемы).

Виды алгоритмов.

Основные виды алгоритмов:

§ алгоритм линейной структуры

§ алгоритм разветвляющейся структуры

§ алгоритм циклической структуры

Линейные алгоритмы.

Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно.

Часто используются не отдельные величины, а массивы- множество связанных однородных величин (например: дата- совокупность 3- х чисел).

Массивом называется упорядоченная совокупность однородных величин, обозначенных каждая одним и тем же именем с различными целочисленными индексами, изменяющимися по порядку (индекс определяет положение элемента в массиве).

Каждый массив определяется именем и числом элементов, например:

T (1: n), где Т – имя массива, n – число элементов массива.

В зависимости от внутреннего строения и взаимного распложения элементов различают разные виды массивов, например, одномерные, двухмерные.

Каждый двухмерный массив определяется именем, числом строк и столбцов.

T(1: m, 1: n), где Т – имя массива, m (n) – число строк (столбцов).

Пример:

Ведомость- это массив. В (1: 4, 1: 3)

№ школы	Число выпускников	Число медалистов

Каждый элемент двухмерного массива определяется номером строки и номером столбца, на пересечении которых он находится.

b₁₁ = 5; b₁₂ = 48

Разветвляющиеся алгоритмы.

Разветвляющимся алгоритмом- называется алгоритм, в котором выбирается один из нескольких возможных путей вычислительного процесса.

Признак разветвляющегося алгоритма- наличие проверки условия. Различают 2 вида условий:

§ Простые

§ Составные

Для составных условий используются логические операции (или логические выражения).

И

Или

Не

Циклические алгоритмы.

Циклическим называется алгоритм, в котором получение результата обеспечивается многократным выполнением одних и тех же операций.

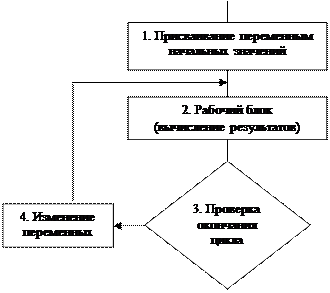Выполнение циклического алгоритма распределяется на этапы (циклы). На каждом цикле вычисляется новое значение алгоритма (в блоке 4) и соответствующее им новое значение результатов рабочих операций (в блоке 2).

Лекция 10
ОСНОВЫ МОДЕЛИРОВАНИЯ

План лекции:

1. Понятие моделирования. Цели и задачи моделирования.
2. Уровни моделирования.
3. Виды моделирования.
4. Моделирование в экономических системах.

Литература:

Понятие моделирования. Цели и задачи моделирования.

Понятие “ модель ” возникло в процессе опытного изучения мира, а само слово “модель” произошло от латинских слов modus, modulus, означающих меру, образ, способ. Первоначальное развитие модели получили в строительном искусстве. Различные вещи, сделанные на основе каких-либо измерений, воспроизводящих что-либо или являющиеся прообразом чего-то, какими-то образцами для других вещей, стали называть моделями.

Можно много привести примеров моделей, при помощи которых описываются и изучаются те или иные явления. Так например, на моделях стали изучать течение водяных потоков, различные гидродинамические явления, происходящие при мощных взрывах, при землетрясениях. Модель дает возможность наблюдать такие явления как, извержение вулкана, возникновение и исчезновение горных систем.

Модели широко применяются в кораблестроении, самолетостроении, ядерной физике, а также строительстве.

Модель – любой аналог (образ) какого-либо объекта, процесса или явления, который используется в качестве "представителя" или "заместителя" этого объекта.

Моделирование – метод научного исследования процессов, объектов, устройств, систем, основанный на построении и изучении моделей с целью исследования характеристик объекта изучения.

Моделирование применяется в качестве:

1. средства обучения и тренировки;
2. средства постановки эксперимента;
3. как инструмент прогнозирования;
4. как средство общения.

Цель моделирования – описание и оптимизация некоторого процесса или явления.

Моделирование по сути является методологией эксперимента. Оно указывает как ставить эксперимент и как обрабатывать его данные, чтобы получить результат, не только достоверный в данном частном случае, но и распространяющийся на группу подобных явлений. Эксперимент имеет два направления:

- планирование эксперимента - методика проведения наблюдений за явлениями (пассивный эксперимент) и одновременно такую стимуляцию изучаемых явлений (активный эксперимент), которая позволила бы наиболее быстро, с меньшим числом опытов найти наиболее характерные зависимости или точки (активный - экстремальный эксперимент). Кроме того, центральное место занимают вопросы организации опытов при учете не одного, а многих влияющих факторов. Такой многофакторный эксперимент должен проводиться согласно четкой схеме, предусматривающей экстремальный и вероятностный подходы к исследованиям;

- обработка данных - методика расчета и построения достоверных характеристик на основе опытных данных, что неизбежно имеет погрешности, отражающиеся, в частности, в “разбросе” опытных точек.

Адекватность модели – степень соответствия модели реальному объекту, процессу или явлению.

Формализация – процесс представления информации в виде некоторой формульной системы или системы счисления.

Исторически первыми моделями, как заместителями некоторых объектов, были символические условные модели. Ими являлись языковые знаки, естественно возникшие в ходе развития человечества и постепенно составившие разговорный язык.

Следующим этапом развития моделирования можно считать возникновение знаковых числовых обозначений. Сведения о результатах счета первоначально сохранился в виде зарубок. Постепенное совершенствование этого метода привело к изображению чисел в виде цифр как системы знаков. Можно предположить, что именно зарубки были прототипом римских цифр I, II, III, V, X.

Дальнейшее развитие знаковых моделей связано с возникновением письменности и математической символики. Наиболее древние письменные тексты, известные в настоящее время, относят примерно к 2000 г. до н. э.(Египет и Вавилон). Есть основания полагать, что вавилоняне уже пользовались понятием подобия прямоугольных треугольников.

Значительное развитие моделирование получает в древней Греции в V-III вв. до н. э. Была создана геометрическая модель Солнечной системы, врач Гиппократ для изучения человеческого глаза воспользовался его физической аналогичной моделью - глазом быка, математик Евклид создал учение о геометрическом подобии.

По мере развития и укрупнения механического производства, металлургии, кораблестроения, градостроения и т. д., все чаще обнаруживается недостаточность геометрического подобия физически однородных объектов для прогнозирования свойств объектов больших размеров на основании свойств объектов меньших размеров.

Первый шаг в развитии учения о подобии при физическом моделировании был сделан И. Ньютоном (1643-1727), который сформулировал условия подобия механических явлений. Далее развитие длительное время шло путем определения частных условий подобия для явлений только определенной физической природы - работы И. П. Кулибина (1735-1818) и Л. Эйлера (1707-1783) в области строительной механики, В. Л. Кирпичева (1845-1913) в области упругости и др.

И наконец, в 1909-1914 гг. Н. Е. Жуковским, Д. Релеем, Ф. Букингемом была сформулирована теорема, позволяющая установить условия подобия явлений любой физической природы.

Параллельно шло развитие логического моделирования в знаковой форме, это прежде всего развитие математики. В конце XVI в. Д. Непер (1550-1617) изобрел логарифмы. В конце XVII в. И. Ньютон и Г. Лейбниц (1646-1716) создали дифференциальное исчисление. Получают развитие численные методы решения различных задач.

К первым вычислительным устройствам можно отнести счеты (XV-XVI в.), логарифмическую линейку (начало XVII в.). Длительное время вычислительные устройства были исключительно механическими - арифмометр, счетно - решающие механизмы и т. п. И только в 30-х гг. нашего столетия начинается развитие электрических аналоговых и цифровых вычислительных устройств.

И первые обобщения двух направлений материального моделирования - а) физического и б) формального с помощью вычислительных устройств были сделаны В. А. Вениковым (1949 г.) и Л. И. Гутенмахером (1949 г.), а затем получили дальнейшее развитие у И. М. Тетельбаума (1959 г.), А. М. Сучилина (1964 г.), П. М. Алабужева (1968 г.). Философские концепции основных общих вопросов моделирования отражены В. А. Штоффом, И. Б. Новиковым, Н. А. Уемовым и др.

Уровни моделирования.

Выделяют три уровня моделирования:

1. Метауровень – уровень сложности в описании объектов исследования, который характеризуется укрупненным рассмотрением протекающих в объекте процессов (проектирование локальных и глобальных сетей, системы движения транспорта);

2. Макроуровень – уровень сложности в описании объектов, который характеризуется рассмотрением физических процессов, протекающих непрерывно во времени, но в дискретном пространстве (моделирование электрических схем, электроэлементов, радиосхем);

3. Микроуровень – уровень сложности в описании объектов, который характеризуется рассмотрением физических процессов в сплошных средах непрерывно во времени (исследование поведения конструкции, электромагнитного поля, температуры поля).

Виды моделирования.

Физическая модель представляет собой модель, элементы которой подобны натуральным объектам исследования, но имеют, как правило, другой масштаб.

Математическое моделирование – изучение объекта путем создания его математической модели. При этом аналитическое математическое моделирование для достижения результата использует раздумья, умозаключения, размышления.

Машинное математическое моделирование подразумевает использование аналоговой или цифровой вычислительной техники.

Имитационное моделирование – процесс конструирования модели реальной системы, постановка эксперимента на этой модели с целью понять поведение системы либо оценить в рамках имеющихся ограничений стратегию поведения этой системы.

Имитационные модели должны обладать следующими свойствами:

1. целенаправленность;

2. простота и понятность пользователю:

3. полнота с точки зрения принятия возможных решений;

4. адекватность;

5. надежность;

6. адаптивность.

Имитационное моделирование выполняется по следующим шагам:

1. определение модели, установка ограничений и определение параметров эффективности;

2. формулирование модели, т.е. переход от реальной системы к некоторой логической схеме;

3. подготовка данных, отбор данных;

4. оценка адекватности модели;

5. трансляция модели, т.е. представление модели на языке, используемом в ЭВМ;

6. стратегическое планирование эксперимента с использованием модели;

7. тактическое планирование, т.е. определение способа проведения серии испытаний;

8. экспериментирование;

9. анализ результата;

10. практическое использование результатов моделирования.

Технология имитационного моделирования сводится к конструированию мысленной модели, имитирующей объекты или процессы по нужным, но не полным показателям. Именно неполнота описания объекта, процесса делает имитационную модель принципиально отличной от математической в традиционном понимании. Это приобретает особую значимость при моделировании социальных процессов, характеризующихся чрезвычайной сложностью как из-за большого числа различных факторов и их взаимосвязей, так и из-за присутствия среди них особых, субъективных факторов.

При помощи имитационного моделирования получены плодотворные результаты в различных областях социального познания (коммерческой деятельности, маркетинге, политике, системе образования, криминалистике и т. д.).

Огромный объем информации, характеризующий объекты социального познания, трудности учета большого числа факторов, логических взаимосвязей и количественных соотношений между ними делают непосильным для человека-исследователя оперирование мысленными моделями социальных процессов. Отсюда возникает необходимость привлечения для моделирования социальных процессов информационных возможностей современной электронно - вычислительной техники.

Так возникло важное направление в научном познании, основанное, с одной стороны, на использовании принципиально новых математических моделей, а с другой - на применении ЭВМ для экспериментирования с этими моделями.

Моделирование в экономических системах.

Использование моделей в экономических информационных системах обеспечивает выполнение таких функций как поддержка и принятие решений, оптимизация, прогнозирование.

Модели, используемые в экономических информационных системах классифицируют:

I. По цели использования:

1. оптимизационные;
2. описательные.

II. По способу оценки моделей:

1. Детерминистские – используют переменные с одним конкретным значением;
2. Стохастические – описывают переменные с несколькими параметрами.

В системах поддержки и принятия решений в зависимости от уровня управления используют следующие модели:

1. Стратегические – (характерны для высшего уровня управления) позволяют устанавливать цели организации, оценивать объём ресурсов, необходимых для этой цели. Характеризуются множеством переменных, данные представлены в сжатой агрегированной форме. Стратегические модели являются детерминистскими, описательными и специализированными.
2. Тактические – (характерны для среднего звена) используются для распределения, контроля имеющихся ресурсов. Являются детерминистскими, оптимизационными, универсальными.
3. Оперативные – используются на низших уровнях управления для поддержки и принятия оперативных решений. Являются детерминистскими, оптимизационными, универсальными.
4. Математические модели – состоят из отдельных модулей, бланков, процедур, реализующих математические методы (линейное программирование, статистический анализ, регрессионный анализ).

Дата добавления: 2014-01-11