CТО. Преобразования Лоренса для координат ивремени

Назовем событием некоторое физическое явление, происходящего в некоторой точке пространства, в некоторый момент времени. Событием будет излучение точечным источником сферической волны. Рассмотрим две инерциальные системы отсчета. Напомним, что каждая точка хар-ется тремя координатами и временем t. В системе К (x, y, z, t), в системе К’ (x’, y’, z’, t’), K’ движется со скоростью 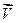. Пусть в некоторый момент времени t’ произошло некоторое событие. Например этой точки достигает фронт сферической волны. Задача-нахожддение координат события в системе К. Произведем синхронизацию часов в системах координат, при t=t’=0. Координаты О и О’ совпадают. Пусть при t=0 из начала координат начало распространение сферическая волна. В системе К уравнение движения записывается так: x²+y²+z²-c²t²=0 (1). Согласно первому постулату Эйнштейна все физические явления во всех инерциальных системах отсчета происходят одинаково и имеют инвариантную форму. (x’)²+(y’)²+(z’)²-(c’)²(t’)²=0 (2), (x’)²+(y’)²+(z’)²-c²(t’)²=0 (3), c=const. Вычитая эти неравенства, получаем (x’)²+(y’)²+(z’)²-c²t²= x²+y²+z²-c²t² (4). Должны получить такие формулы преобразования координат при переходе из одной системы в другую, где выполняется (4), полученное нами из постулатов Эйнштейна. Изложим те преобразования к формулам преобразования, которые следуют из общих соображений. Во-первых, формулы преобразования должны быть линейными. Во-вторых, т. к. движение происходит вдоль оси x, то можно предположить y’=y, z’=z (5). При t=0 начало координат К и К’ совпадают, т. е. координата плоскости x’ то x=Vt. Следовательно, мы можем написать x’=α(V)(x-Vt) (6), здесь α=const, зависит от времени. Дальше наступает наиболее неочевидное предположение. Предположим, что t’ является линейной функцией, а именно t’=βt+γx (7). Здесь β и γ=const могут зависеть от V. Подставим (5), (6) и (7) в (4): α²(x-Vt)²+y²+z²-c²(βt+γx)²= x²+y²+z²-c²t² (8). Возводим в квадрат левую часть, появляется структура типа Ax²+Bxt+Ct²=0 (9). Это равенство возможно для любого x и t, только при A=B=C=0. α²-c²γ²=1 (11), α²V²-c²β²=-c² (12), α²V+ c²βγ=0 (13), α²V=-c²βγ, γ=-α²V/c²β (14), подставим (14) в (11), α²-c²(α⁴V²/c²β²)=1, α²c²-β²-α⁴V²=c²β², α²V-c²β²=-c²β²/α² (15), -c²=-c²β²/α², α=β, α²(V²-c²)=-c², α²=c²/(V²-c²)=1/(1-V²/c²). α=β=1/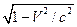(16). Из (14) получаем: γ=-α²V²/c²β=-V/(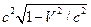) (17). Подставляя const в предыдущие формулы мы получаем преобразования Лоренца: x’=(x-Vt)/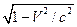,y’=y, z’=z и t’=(t-Vx/c²)/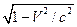} (I).

▼ Формулы преобразования координат времени (I) носят названия формул преобразования Лоренца. Обратные формулы получаются из (I) заменой штрихованной на не штрихованную (V→V’). x=(x’-Vt’)/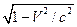, y=y’, z=z’ и t=(t’-Vx’/c²)/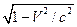} (II).

Дата добавления: 2014-01-11