Минимизация случайной погрешности

Уменьшить случайную погрешность можно, определяя оценку математического ожидания многократных наблюдений измеряемой величины 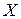. В этом случае за результат измерения, как правило, принимается среднее арифметическое результатов наблюдений

.

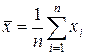Поскольку 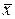определяется по конечному числу наблюдений, то является случайной величиной.

Дисперсия среднего арифметического результатов наблюдений 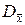в 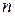раз меньше дисперсии однократного наблюдения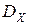

.

Поэтому, принимая за результат измерения 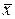, можно ожидать уменьшения случайной погрешности.

Границы погрешности среднего арифметического будут определяться выражением

.

Для определения границ погрешности среднего арифметического необходимо знать его закон распределения.

Центральная предельная теорема теории вероятности гласит: если имеется 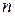независимых случайных величин 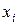, распределенных по одному и тому же закону с математическим ожиданием 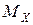и дисперсией 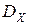, то при неограниченном увеличении 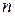закон распределения суммы 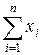неограниченно приближается к нормальному.

Считается, что при центральная предельная теорема соблюдается, поэтому в этом случае значения доверительного коэффициента берутся из таблиц для нормального распределения.

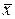Если , то распределение уже нельзя считать нормальным. В этом случае 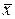распределено по закону распределения Стьюдента с числом степеней свободы .

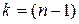Плотность распределения Стьюдента имеет вид

.

С ростом 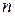распределение Стьюдента приближается к нормальному и при уже неотличимо от него.

Таким образом, если известно, что результаты отдельных наблюдений распределены по нормальному закону, то при числе наблюдений 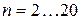при определении границ случайной погрешности доверительный коэффициент 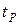берется из таблиц распределения Стьюдента для ()–й степени свободы и заданной вероятности .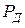

Дата добавления: 2014-01-11