Обнаружение систематических погрешностей

Если результат наблюдения 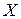содержит систематическую погрешность 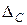, то оценка математического ожидания результата наблюдения

.

В отличие от случайных погрешностей 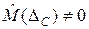. Поэтому обнаружение и минимизация систематических погрешностей таким же образом, как и случайных, не представляется возможным.

Способы обнаружения систематической погрешности различаются в зависимости от характера ее изменения.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от среднего арифметического, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основе априорных знаний об этих погрешностях, получаемых, например, при поверке СИТ, которая может осуществляться двумя способами:

1) с помощью эталонной меры. Измеряемая величина при поверке воспроизводится эталонной мерой, значение которой известно. Поэтому разность между средним арифметическим результата наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями, равна искомой систематической погрешности. ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени (межповерочного интервала) и их независимостью от внешних условий. Если СИТ имеет возможность измерять нулевое значение физической величины, то последнее (при аддитивной абсолютной погрешности СИТ) можно использовать вместо эталонной меры. Показания СИТ при отсутствии измеряемой величины будут равны искомой систематической погрешности;

2) с помощью эталонного СИТ. Произвольная по значению физическая величина измеряется одновременно с помощью исследуемого и эталонного СИТ. Разность между их результатами измерений равна систематической погрешности исследуемого СИТ.

Переменные систематические погрешности, существенные по сравнению со случайными погрешностями, можно обнаружить, построив график последовательности результатов наблюдений или их отклонений от среднего арифметического. При прогрессивной систематической погрешности последовательность результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию, а при периодической систематической погрешности прослеживаются колебания средних значений случайных отклонений.

Если систематическая переменная погрешность соизмерима со случайной, ее можно обнаружить с помощью специальных методов обработки. В этом случае можно воспользоваться аппаратом дисперсионного анализа, который основан на исследованиях закономерностей соотношений дисперсий и средних арифметических разных групп наблюдений.

Наличие систематических погрешностей определяют по значению смещения средних арифметических, для чего применяются различные методы, среди которых наиболее известны методы Аббе и Фишера.

Дата добавления: 2014-01-11