Графическая иллюстрация

Проиллюстрируем полученные аналитические зависимости графически. На рисунке 3.1 показана графическая зависимость

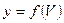при .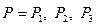

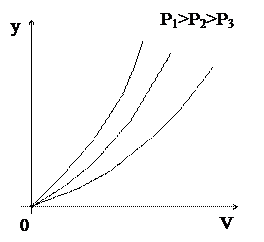Рисунок 3.1 – Зависимость 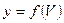при .

Из рисунка видно, что при увеличении емкости обслуживающего пучка линий при фиксированных потерях интенсивность поступающей нагрузки увеличивается. Это положение в равной степени справедливо и для обслуженной нагрузки.

На рисунке 3.2 показана зависимость удельной пропускной способности от емкости пучка при разной вероятности потерь.

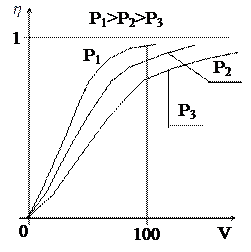Рисунок 3.2 – Зависимость 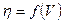при .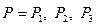

Из графика видно, что с увеличением емкости пучка при фиксированных потерях удельная пропускная способность каждой линии возрастает. Возрастает она и при увеличении вероятности потерь при фиксированной емкости пучка. Приведенный анализ позволяет сделать важный для практики вывод.

Для повышения использования каждой линии пучки нужно укрупнять.

Из рисунка 3.2 видно, что наибольший эффект дает увеличение емкости пучков до 100 линий. Дальнейшее укрупнение пучков не приводит к существенному увеличению пропускной способности каждой линии.

Из приведенных графиков видно, что предельная пропускная способность одной линии пучка (однолинейная система) составляет один Эрланг. В реальных системах за счет неизбежного простоя линий всегда 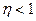Эрл.

3.5 Обслуживание примитивного потока вызовов

Примитивный поток является частным случаем симметричного потока, поэтому воспользуется полученными ранее выражениями для .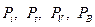

.

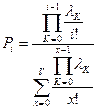Преобразуем числитель

.

Преобразуя по аналогии знаменатель, получим

; .

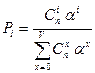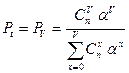Потери по вызовам

,

.

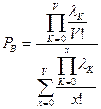Тогда

.

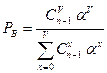В приведенных выражениях 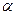- параметр потока одного свободного источника. На практике удобнее пользоваться величиной 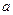- удельной нагрузкой, поступающей от одного источника. Найдем связь между 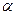и 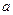. Для этого рассмотрим систему без потерь. В этом случае достаточно ограничиться рассмотрением однолинейной модели, т.е. .

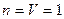В этом случае величина 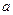может трактоваться как вероятность занятости линии в однолинейном пучке - .

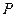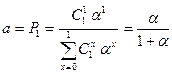или .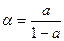

Преобразуем полученные выше выражения для 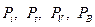, используя величину ,

.

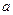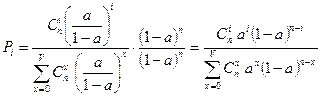Потери по времени

.

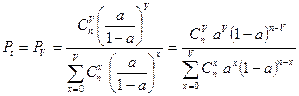Потери по вызовам

.

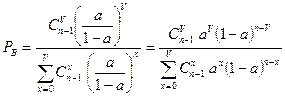Потери по нагрузке

; ; .

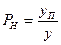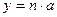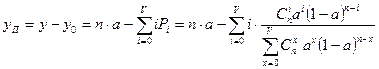Подставляя полученные выражения для и 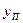в формулу для потерь по времени, после преобразований получим

.

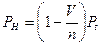Полученные выше выражения для вероятностей 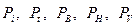называются формулами Энгсета. Выражения для 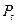и табулированы [13]. При пользовании таблицами Энгсета следует иметь ввиду следующее.

Поскольку функци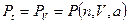и

и ,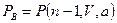

имеют один и тот же вид, то изменяя число источников можно по одной какой-либо таблице получить оба вида потерь. Из приведенных выражений видно, что в модели Энгсета потери по времени больше потерь по вызовам, которые, в свою очередь, больше потерь по нагрузке

.

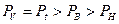Сравним с первой формулой Эрланга, в которой

.

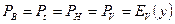Дата добавления: 2014-01-11