Обучение персептрона

Способность искусственных нейронных сетей обучаться является их наиболее интригующим свойством.

Используя критерий линейной разделимости, можно решить, способна ли однослойная нейронная сеть реализовывать требуемую функцию. Даже в том случае, когда ответ положительный, это принесет мало пользы, если у нас нет способа найти нужные значения для весов и порогов. Чтобы сеть представляла практическую ценность, нужен систематический метод (алгоритм) для вычисления этих значений. Розенблатт сделал это в своем алгоритме обучения персептрона вместе с доказательством того, что персептрон может быть обучен всему, что он может реализовывать.

Обучение может быть с учителем или без него. Для обучения с учителем нужен «внешний» учитель, который оценивал бы поведение системы и управлял ее последующими модификациями. При обучении без учителя, сеть путем самоорганизации делает требуемые изменения. Обучение персептрона является обучением с учителем.

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае - ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.

На рис. 13 показана такая персептронная конфигурация. Допустим, что вектор Х является образом распознаваемой демонстрационной карты. Каждая компонента (квадрат) Х - (х₁, х₂,..., х₉) - умножается на соответствующую компоненту вектора весов W (w₁,..., w₉). Эти произведения суммируются. Если сумма превышает порог, то выход нейрона У равен единице (индикатор зажигается), в противном случае он -ноль. Эта операция компактно записывается в векторной форме как У = XW, а после нее следует пороговая операция.

Для обучения сети образ Х подается на вход и вычисляется выход У. Если У правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.

Чтобы увидеть, как это осуществляется, допустим, что демонстрационная карта с цифрой 3 подана на вход и выход У равен 1 (показывая нечетность). Так как это правильный ответ, то веса не изменяются. Если, однако, на вход подается карта с номером 4 и выход У равен единице (нечетный), то веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если карта с номе­ром 3 дает нулевой выход, то веса, присоединенные к единичным входам, должны быть увеличены, чтобы скорре­ктировать ошибку.

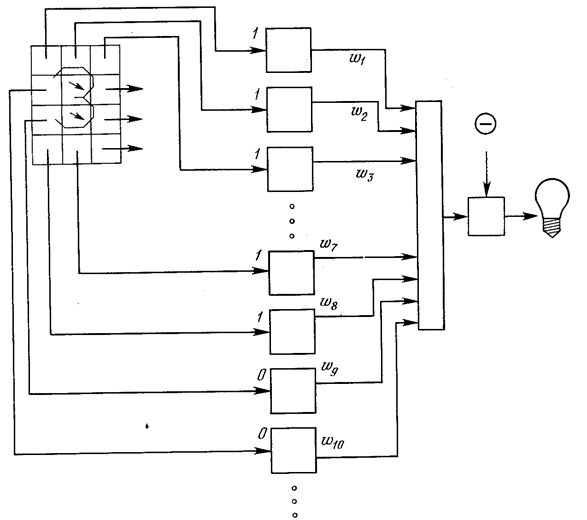
Рис. 13. Персептронная система распознавания изображений.

Этот метод обучения может быть подытожен следующим образом:

1. Подать входной образ и вычислить Y.

2. а. Если выход правильный, то перейти на шаг 1;

б. Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или

в. Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.

3. Перейти на шаг 1.

За конечное число шагов сеть научится разделять карты на четные и нечетные, при условии, что множество цифр линейно разделимо. Это значит, что для всех нечетных карт выход будет больше порога, а для всех четных -меньше. Отметим, что это обучение глобально, т.е. сеть обучается на всем множестве карт. Возникает вопрос о том, как это множество должно предъявляться, чтобы минимизировать время обучения. Должны ли элементы множества предъявляться последовательно друг за другом или карты следует выбирать случайно?

Дельта-правило

Важное обобщение алгоритма обучения персептрона, называемое дельта-правилом, переносит этот метод на непрерывные входы и выходы. Чтобы понять, как оно было получено, шаг 2 алгоритма обучения персептрона может быть сформулирован в обобщенной форме с помощью введения величины δ, которая равна разности между требуемым или целевым выходом Т и реальным выходом А

δ = Т - А. (9)

Случай, когда δ =0, соответствует шагу 2а, когда выход правилен и в сети ничего не изменяется. Шаг 2б соответствует случаю δ > 0, а шаг 2в случаю δ < 0.

В любом из этих случаев персептронный алгоритм обучения сохраняется, если δ умножается на величину каждого входа х. и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент «скорости обучения», который умножается на δ, что позволяет управлять средней величиной изменения весов.

В алгебраической форме записи:

Δ_i = η δx_i;

w _i .(n+1)= w _i .(n+1)+ Δ_i;

где Δ_i - коррекция, связанная с i-м входом хi;

w _i .(n+1) - значение веса i после коррекции; w _i .(n) -значение веса i до коррекции.

Дельта-правило модифицирует веса в соответствии с требуемым и действительным значениями выхода каждой полярности, как для непрерывных, так и для бинарных входов и выходов. Эти свойства открыли множество новых приложений.

Дата добавления: 2014-01-11