
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тоді можна записати, що
|
|
|
|
L · у = b. (4)
Розв’язування системи (1) або (2) відбувається в два етапи: спочатку розв’язується система L · у = b, а потім U · x = у. Така послідовність розв’язку дає перевагу методу (в порівнянні з методом Гауса) – якщо потрібно розв’язати декілька систем з однією і тією ж матрицею А, задача суттєво спрощується, оскільки зберігаються матриці L та U.
Розв’язок системи L · у = b називається прямим ходом, а системи U · x = у – оберненим ходом.
Розглянемо прямий хід. Завдяки спеціальній формі матриці L вектор у можна легко визначити. Для цього (4) перепишемо у вигляді системи рівнянь

Звідси можна одержати, що в загальному вигляді
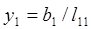 (5)
(5)
 для
для 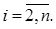
При оберненому ході вектор х визначається з системи рівнянь (3)
x 1 + u 12 x 2 + u 13 x 3 + … + u 1 n xn = y 1
x 2 + u 23 x 3 + … + u 2 n xn = y 2
x 3 + … + u 3 n xn = y 3
………………………………
xn = yn.
Починаючи з останнього рівняння, можна послідовно знайти компоненти вектора х. В загальному вигляді вони визначаються за формулами
 для
для  (6)
(6)
Тепер розглянемо LU – розклад матриці А.
У варіанті методу, що називається методом Крута, використовується наступна послідовність знаходження елементів матриць L та U ( ) – де k – крок.
) – де k – крок.
Для всіх 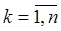
 де
де  (7)
(7)
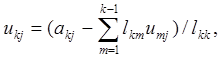 де
де  (8)
(8)
Домовимось, як звичайно, вважати значення суми рівним нулю, якщо верхня границя (межа) сумування менша від нижньої.
Алгоритм
1) k =1
Обчислюємо
 для всіх
для всіх 
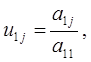 для всіх
для всіх  .
.
2) k = k + 1
 де
де 
 де
де  .
.
Продовжуємо до тих пір, доки k = n.
Зауваження щодо алгоритму побудови програми:
1) Необхідні в цих співвідношеннях значення елементів матриць L та U обчислюються на попередніх етапах процесу.
2) Кожний елемент aij матриці А потрібен тільки для обчислення відповідних елементів матриці L та U (тобто, в подальшому процесі aij не потрібні). Оскільки нульові елементи матриць L та U, а також одиничну діагональ матриці U запам’ятовувати не потрібно, тобто в процесі обчислення матриці L та U можуть бути записані на місце матриці А. Причому матриця L розташована в нижньому трикутнику (i ≥ j), U – відповідно в верхньому трикутнику (i < j) матриці А.
3) Розклад матриці А на матриці L та U, як правило, об’єднують з прямим ходом. Може бути використана наступна послідовність обчислень: спочатку обчислюється перший стовпець матриці L, потім перший рядок матриці U та перший елемент вектора у; далі – другий стовпець матриці L, другий рядок матриці U та другий елемент вектора у і т.д.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 310; Нарушение авторских прав?; Мы поможем в написании вашей работы!