Базис и координаты вектора

B

А

A+b

Линейные операции над векторами.

Определение 5.4. Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

b

a

Замечание. Такое правило сложения векторов называют правилом треугольника.

Свойства сложения:

Свойство 1. a + b = b + a.

Доказательство. Приложим векторы а и b к общему началу и рассмотрим параллелограмм

AOBC. Из определения 5.4 и треугольника ОВС следует, что ОС= b+a, а из треугольника

ОАС – ОС= а+b. Свойство 1 доказано.

В а С Замечание. При этом сформулировано еще одно правило

b b сложения векторов – правило параллелограмма: сумма

a+b= векторов a и b есть диагональ параллелограмма, построенно-

=b+a го на них как на сторонах, выходящая из их общего начала.

О А

Свойство 2. (a+b)+c=a+(b+c).

b Доказательство. Из рисунка видно, что

A a + b B (a+b)+c =(OA+AB)+BC=OB+BC=OC,

a a+(b+c)=OA+(AB+BC)=OA+AC=OC.

Свойство 2 доказано.

b+с

O c С

Свойство 3. Для любого вектора a существует нулевой вектор О такой, что a +О=а.

Доказательство этого свойства следует из определения 5.4.

Свойство 4. Для каждого вектора a существует противоположный ему вектор a ^/ такой, что а+а ^/=О.

Доказательство. Достаточно определить a ^/ как вектор, коллинеарный вектору a, имеющий одинаковую с ним длину и противоположное направление.

Определение 5.5. Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

a a-b

Определение 5.6. Произведением k a вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный | k || a |, и направление, совпадающее с направлением а при k >0 и противоположное а при k<0.

Свойства умножения вектора на число:

Свойство 1. k( a + b ) = k a + k b.

Свойство 2. (k + m) a = k a + m a.

Свойство 3. k(m a ) = (km) a.

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = k a.

Определение 5.7. Линейной комбинацией векторов а_1, а₂,…,а_n называется выражение вида: k₁ a₁ + k₂ a₂ +…+ k_n a_n, (5.1)

где k_i – числа.

Определение 5.8. Векторы а_1, а₂,…,а_n называются линейно зависимыми, если найдутся такие числа k₁, k₂,…, k_n, не все равные нулю, что соответствующая линейная комбинация векторов равна нулю, т.е. k₁ a₁ + k₂ a₂ +…+ k_n a_n = 0. (5.2)

Если же равенство (5.2) возможно только при всех k _i = 0, векторы называются линейно независимыми.

Замечание 1. Если система векторов содержит нулевой вектор, то она линейно зависима.

Замечание 2. Если среди n векторов какие-либо (n -1) линейно зависимы, то и все n векторов линейно зависимы.

Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Определение 5.9. Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Замечание 4. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.

Определение 5.10. Два линейно независимых вектора на плоскости (или три линейно независимых вектора в пространстве) образуют базис, если любой вектор плоскости (пространства) может быть представлен в виде их линейной комбинации. Числовые коэффициенты этой линейной комбинации называются координатами данного вектора в рассматриваемом базисе:

если a, b, c – базис и d = k a + m b + p c, то числа k, m, p есть координаты вектора d в базисе a, b, c.

Свойства базиса:

1. Любые два неколлинеарных вектора образуют базис на плоскости, а любые три некомпланарных вектора – базис в пространстве.
2. Разложение данного вектора по данному базису единственно, т.е. его координаты в данном базисе определяются единственным образом.
3. При сложении двух векторов их координаты относительно любого базиса складываются.
4. При умножении вектора на число все его координаты умножаются на это число.

Определение 5.11. Проекцией вектора АВ на ось u называется длина направленного отрезка А^/В^/ оси u, где А^/ и В^/ - основания перпендикуляров, опущенных из точек А и В на ось u.

Обозначение: пр_u а.

Свойства проекции:

1. Пр_u a = | a | cosφ, где φ – угол между а и осью u.
2. При сложении двух векторов их проекции на любую ось складываются.
3. При умножении вектора на число его проекция на любую ось умножается на это число.

Замечание. Свойства 2 и 3 назовем линейными свойствами проекции.

Рассмотрим декартову систему координат, базис которой образуют в пространстве три попарно ортогональных единичных вектора i, j, k. Тогда любой вектор d может быть представлен в виде их линейной комбинации:

d = X i + Y j +Z k. (5.3)

Определение 5.12. Числа X, Y, Z называются декартовыми координатами вектора d.

Замечание. Декартовы координаты вектора равны его проекциям на оси Ох, Оу и Оz декартовой системы координат.

Определение 5.13. Косинусы углов, образованных вектором о осями декартовой системы координат, называются его направляющими косинусами.

Свойства направляющих косинусов:

1. X = | d | cos α, Y = | d | cos β, Z = | d | cosγ.
2. , , .
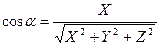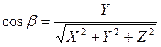3. cos²α + cos²β + cos²γ = 1.

Дата добавления: 2014-01-11