Функция распределения

Определение 4.4. Функцией распределения F (x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:

F (x) = p (X < x). (4.1)

Свойства функции распределения.

1) 0 ≤ F (x) ≤ 1. Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.

2) Функция распределения является неубывающей функцией, то есть F (x ₂) ≥ F (x ₁) при х ₂ > x ₁. Это следует из того, что F (x ₂) = p (X < x ₂) = p (X < x ₁) + p (x ₁ ≤ X < x ₂) ≥ F (x ₁).

3) В частности, если все возможные значения Х лежат на интервале [ a, b ], то F (x) = 0 при х ≤ а и F (x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное.

4) Вероятность того, что случайная величина примет значение из интервала [ a, b ], равна разности значений функции распределения на концах интервала:

p (a < X < b) = F (b) – F (a).

Справедливость этого утверждения следует из определения функции распределения (см. свойство 2).

Для дискретной случайной величины значение F (x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.

Пример. Найдем F (x) для предыдущего примера:

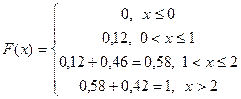
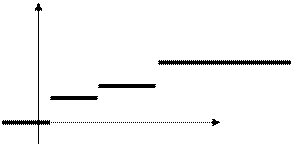
Соответственно график функции распределения имеет ступенчатый вид:

Биномиальное распределение.

Вернемся к схеме независимых испытаний и найдем закон распределения случайной величины Х – числа появлений события А в серии из п испытаний. Возможные значения А: 0, 1, …, п. Соответствующие им вероятности можно вычислить по формуле Бернулли:

(4.2)

(p – вероятность появления А в каждом испытании).

Такой закон распределения называют биномиальным, поскольку правую часть равенства (4.2) можно рассматривать как общий член разложения бинома Ньютона:

Пример. Составим ряд распределения случайной величины Х – числа попаданий при 5 выстрелах, если вероятность попадания при одном выстреле равна 0,8.

р (Х =0) = 1·(0,2)⁵ = 0,00032; р (Х= 1) = 5·0,8·(0,2)⁴ = 0,0064; р (Х =2) = 10·(0,8)²·(0,2)³ = 0,0512; р (Х =3) = 10·(0,8)³·(0,2)² = 0,2048; р (Х =4) = 5·(0,8)⁴·0,2 = 0,4096; р (Х =5) = 1·(0,8)⁵ = 0,32768. Таким образом, ряд распределения имеет вид:

х
р	0.00032	0.0064	0.0512	0.2048	0.4096	0.32728

Распределение Пуассона.

Рассмотрим дискретную случайную величину Х, принимающую только целые неотрицательные значения (0, 1, 2,…, т,…), последовательность которых не ограничена. Такая случайная величина называется распределенной по закону Пуассона, если вероятность того, что она примет значение т, выражается формулой:

, (4.3)

где а – некоторая положительная величина, называемая параметром закона Пуассона.

Покажем, что сумма всех вероятностей равна 1:

(использовано разложение в ряд Тейлора функции е^х).

Рассмотрим типичную задачу, приводящую к распределению Пуассона. Пусть на оси абсцисс случайным образом распределяются точки, причем их распределение удовлет-воряет следующим условиям:

1) вероятность попадания некоторого количества точек на отрезок длины l зависит только от длины отрезка и не зависит от его расположения на оси (то есть точки распределены с одинаковой средней плотностью);

2) точки распределяются независимо друг от друга (вероятность попадания какого-либо числа точек на данный отрезок не зависит от количества точек, попавший на любой другой отрезок);

3) практическая невозможность совпадения двух или более точек.

Тогда случайная величина Х – число точек, попадающих на отрезок длины l – распре-делена по закону Пуассона, где а – среднее число точек, приходящееся на отрезок длины l.

Замечание. В лекции 3 говорилось о том, что формула Пуассона выражает биномиальное распределение при большом числе опытов и малой вероятности события. Поэтому закон Пуассона часто называют законом редких явлений.

Дата добавления: 2014-01-11