Назначение и расчет переходных посадок, примеры применения

В переходных посадках может возникать как зазор, так и натяг. Они обеспечивают относительно высокие требования к центрированию и возможность частой разборки соединения. Зазоры и натяги в таких посадках невелики. Рекомендуется назначать в таких посадках квалитет от 4 -го до 8-го, но квалитет вала должен быть на единицу точнее, чем квалитет отверстия.

Цель расчета переходных посадок заключается в определении вероятности появления зазоров и натягов для заданного расположения полей допусков сопрягаемых деталей и известном номинальном размере.

Алгоритм расчета переходных посадок:

1) определение характерных размеров полей допусков сопрягаемых деталей:

.

2) определение поля рассеяния действительных диаметров сопрягаемых деталей относительно соответствующих полей допусков для отверстия и вала соответственно:

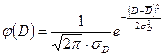, (15.1)

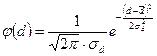. (15.2)

Для расчетов по формулам необходимо знать две статические характеристики, математическое ожидание 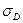и среднее квадратичное отклонение 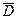для отверстия и для вала 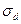и .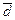

Наиболее вероятный диаметр, как известно, находится в середине поля допуска:

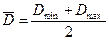, (15.3)

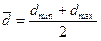. (15.4)

С учетом того, что квантинормальное распределение равно трем и функция четная в данном случае, то среднее квадратичное отклонение можно определить следующим образом:

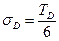, (15.5)

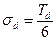. (15.6)

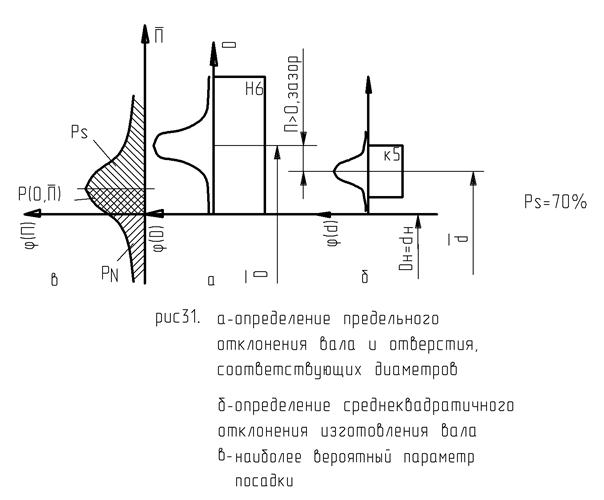
Зная оба параметра соответствующего распределения, можно построить это распределение. Для этого выберем систему координат так, чтобы график был симметричен, и ось ординат 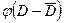проходила через середину поля допуска 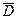, тогда максимум будет находиться на оси координат (рис. 31). Аналогично строится вероятностное распределение и в системе вала. Отметим, что таким образом был получен не только качественный, но и численный график, следовательно, поле допуска соответствующей детали обеспечивает вероятность равную 0,997.

3) нахождение распределения параметра посадки:

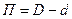. (15.7)

Известно, что поступление вала и отверстия на сборку является случайным событием, поэтому появление в этой сборке зазора или натяга тоже является случайным событием. Тогда:

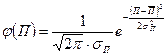. (15.8)

Для нахождения вида этой кривой необходимо вычислить два параметра:

наиболее ожидаемый параметр посадки

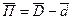(15.9)

и дисперсия

. (15.10)

Формула (15.10) получена из следующих соображений. В общем виде косвенное случайное событие 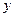связано с некоторыми прямыми событиями:

,

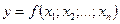а для каждого прямого события 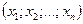известна дисперсия (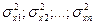) соответственно.

Дисперсия косвенного события имеет форму полного дифференциала

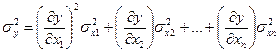. (15.11)

В рассматриваемом случае:

, , ,

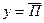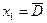а производные

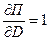и .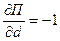

Следовательно,

.

Когда необходимые параметры найдены, можно построить график плотности распределения параметра посадки. Максимум данной функции будет находиться в месте наиболее вероятного параметра посадки, т.к. в данном случае 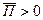, то 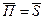и максимум будет в месте наиболее вероятного зазора.

Из определения натяга и зазора следует, что площадь под кривой распределения выше нулевой линии соответствует зазору, ниже нулевой линии - натягу.

4) определение вероятности появления соответствующих параметров посадки. На интервале 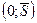эта вероятность вычисляется по формуле Лапласа:

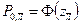. (15.12)

Здесь квантиль 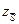равен отношению интервала 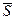к среднему квадратичному отклонению:

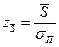. (15.13)

Следует обратить внимание на то, что берется не двойная функция Лапласа, а с единичным коэффициентом, т.к. рассматривается только половина симметричного интеграла.

В целом вероятность появления зазора в таком соединении может быть определена как сумма

.

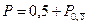Вероятность появления натяга тогда равна

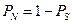. (15.14)

Дата добавления: 2014-01-11