Обработка результатов косвенных измерений

Обработка результатов измерений. Однократные и многократные из­мерения. Исключение грубых и систематических погрешностей изме­рений. Оценка случайной составляющей погрешности измерений.

Алгоритм.

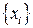- множество случайных результатов измерения (повторные опыты, из которых исключена систематическая составляющая погрешности измерения).

С помощью формулы (27.12) находится математическое ожидание, используя уравнение (27.13) - множество случайных погрешностей измерений, с помощью формулы (27.14) – величина среднего квадратичного отклонения и исключаются промахи:

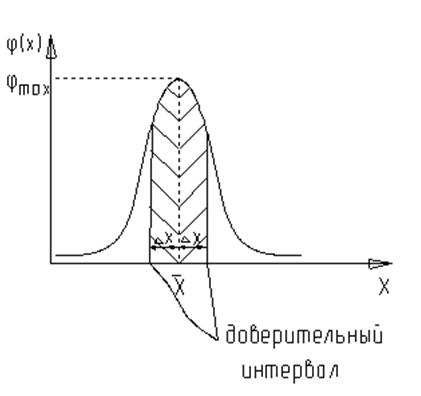
На графике изображены результаты повторных опытов. После построения гистограммы или математической обработки наносится соответствующая кривая распределения Гаусса, максимум которой находится в точке соответствующей математическому ожиданию, вид кривой определяется двумя статическими параметрами – математическим ожиданиям и средним квадратичным отклонением.

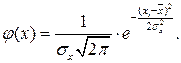(27.16)

Зная кривую, можно найти вероятность появления некоторого измерения в каком - либо интервале, в отличие от других измерений, вводится понятие доверительного интервала, который является симметричным относительно математического ожидания и относительного его определяется доверительная вероятность. Функция Гаусса четная, следовательно, можно определить вероятность появления результата единичного измерения в интервале, равного удвоенной функции Лапласа от квантиля нормального распределения:

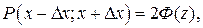(27.17)

квантиль

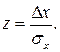(27.18)

В технических измерениях в качестве доверительной вероятности обычно используется величина 0,95, что соответствует удвоенному квантилю нормального распределения:

z = 2,

,

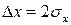P(2)=0,95.

Иногда используется коэффициент значимости, равный разности между единицей и доверительной вероятностью

Интервал Δx называется в этом случае – доверительным, а вероятность - доверительная вероятность.

Пусть было проведено 1000 измерений, выбрана вероятность 0,95, необходимо определить промахи в данном множестве х. Закономерно, что 950 измерений лежат внутри доверительного интервала, а 50 могут быть за пределами, те измерения, которые попали за пределами доверительного интервала, являются закономерными для того количества измерений. При 100 измерениях 95 должны входить в интервал, при 10 измерениях за пределами может лежать одно рядом с границами интервала, либо ничего. Чем дальше измерения отклоняются от математического ожидания, тем меньше вероятность его появления, и тем больше вероятность того, что это измерение - промах,.

Для проверки на промах из всего множества случайных величин выбирается результат, имеющий максимальное отклонение от математического ожидания - 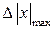, находится его квантиль - 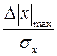, которое если не превышает критерия Шовена S(n), зависящего от числа измерений, то результат не считается промахом:

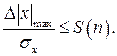(27.19)

Если условие не выполняется, то результат этого измерения исключается, и обработка повторяется с новыми значениями 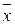, до тех пор, пока все промахи не будут исключены. Затем результат измерения записывается в форме:

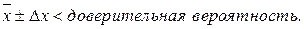
Пусть косвенное измерение у связано с т прямыми измерениями известной зависимостью:

,

причем каждое из них проведено п раз.

Очевидно, т погрешностей, например, первого измерения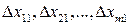
вызовут определенную погрешность косвенного из­мерения 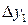. Обычно величины 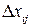весьма малы, а прямые измерения x_i можно считать независимыми. Тогда связь прямых
и косвенных погрешностей в первом измерении определяется из­вестным выражением полного дифференциала функции несколь­ких переменных: 1г

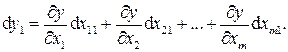(27.20)

Аналогичные выражения можно записать и для остальных п из­мерений:

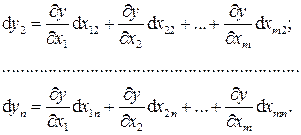(27.21)

Возведем эти выражения в квадрат, пренебрегая смешанными членами типа d x_ij d x_ki, и разделим на (п - 1).

Тогда в левой части получим квадрат среднего квадратичного отклонения косвенного измерения, в правой части, после простых преобразований, - со­ответствующие параметры прямых измерений:

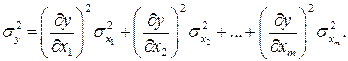(27.22)

Аналогичную связь можно получить и между другими парамет­рами точности прямых и косвенных измерений.

Найдем, например, погрешность среднеарифметического, рас­сматривая его как косвенное, а Х₁, Х₂,..., Х_N как прямые с одина­ковым средним квадратичным отклонением σ. Их связь дается выражением:

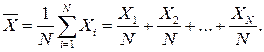(27.23)

Но 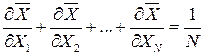и в соответствии с (27.22) получаем:

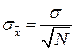. (27.24)

Часто встречается случай, когда косвенное измерение представ­ляет произведение или частное прямых измерений. Например, при определении плотности вещества цилиндра

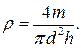(27.25)

Найдем соответствующие производные

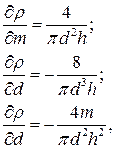(27.26)

подставим их в (1) и разделим на (2):

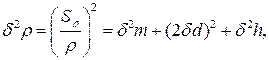(27.27)

где 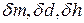- относительные погрешности прямого изме­рения массы, диаметра и высоты цилиндра.

Таким образом, если косвенное измерение представляет собой частное и произведение прямых, то следует складывать квадраты не средних квадратичных отклонений σ², а относительных погреш­ностей δ², причем коэффициент перед относительной погрешностью, равен показателю степени соответствующего прямого измерения (см. формулы (27.25), (27.27).

Дата добавления: 2014-01-11