Модель криптографической системы

Простейшую модель криптографической системы можно изобразить так, как показано на рисунке (см. рис. 1.). Таким образом, имеется некая информационная система, включающая двух или более абонентов (законных пользователей) и канал (или каналы), по которым абоненты могут обмениваться сообщениями. Имеется также возможность появления противника, т.е. незаконного пользователя. Противник может перехватывать сообщения, передаваемые абонентами друг другу.

Рис. 1 Простейшая модель криптосистемы

Здесь необходимы следующие пояснения. Во - первых, противник может быть как внешним (т.е. не входить в число абонентов системы), так и внутренним (быть абонентом системы). В последнем случае этот абонент считается незаконным пользователем, если он пытается получить доступ к сообщениям, на которые не имеет права (например, конфиденциальные сообщения, которыми обмениваются другие абоненты). Во - вторых, противник может перехватывать сообщения с разными целями — например, с целью разглашения перехватываемой информации (использование этой информации в своих целях или передача информации другому лицу), подмены или имитации сообщения и т.д.

Подобные цели называются угрозами. Для защиты от различных видов угроз необходимо применять различные криптографические методы.

Рассматриваемая нами задача обеспечения конфиденциальности информации представляет собой задачу защиты от угрозы разглашения.

Следует иметь в виду, что описанная модель может применяться и в случаях, внешне отличных от обмена сообщениями. Например, при защите данных, хранящихся на компьютере, можно считать, что абонент А и абонент Б — одно и то же лицо, работающее с данными в разные моменты времени. В этом случае «каналом» является жесткий диск компьютера, на котором хранятся данные.

Итак, рассматривается модель, в которой противник имеет доступ к каналу передачи сообщений. Поэтому абонент, передающий сообщение (отправитель) должен перед отправкой преобразовать исходную информацию (открытый текст) в закрытый текст (который называется шифртекстом, зашифрованным текстом или криптограммой). Преобразование открытого текста в шифртекст называется шифрованием (часто используется также термин зашифрование). Абонент, получивший такой зашифрованный текст (получатель), с помощью обратного преобразования (расшифрования, расшифровки) восстанавливает исходный открытый текст.

Процедуры шифрования и расшифрования используют некоторые секретные данные, называемые ключами, причем в некоторых криптосистемах ключ шифрования и ключ расшифрования совпадают, а в других — различаются. Ключи известны только абонентам криптосистемы, причем для обмена данными с различными пользователями один и тот же абонент может использовать различные ключи. Противник не знает ключ расшифрования, но может попытаться вскрыть шифр, т.е. либо подобрать ключ, либо преобразовать зашифрованный текст в открытый каким –либо другим способом.

Методы вскрытия шифров называются криптоанализом, а противник, применяющий эти методы — криптоаналитиком. Успех криптоанализа зависит как от свойств криптографической системы, так и от имеющихся у противника ресурсов (время, мощность вычислительных машин и т.п.).

Способность шифра (криптосистемы) противостоять попыткам взлома (атакам) называется стойкостью шифра.

Существуют абсолютно стойкие системы шифрования, однако они очень не удобны и требуют больших затрат при использовании. Ни одна из широко используемых на практике систем шифрования не является абсолютно стойкой. Это означает, что если противник обладает неограниченными ресурсами и достаточно широкими возможностями для атаки (например, имеет доступ к некоторым открытым текстам и соответствующим им шифртекстам, полученным с использованием одного и того же ключа), то рано или поздно он сможет взломать шифр. Однако если выгода от использования полученной информации будет меньше, чем затраты на взлом, противник вряд ли будет этим заниматься. Поэтому при выборе алгоритма шифрования необходимо точно оценить соотношение ценности защищаемой информации, стойкости шифра и удобства его использования — иначе затраты на защиту информации могут превысить стоимость самой информации.

Формальная модель и классификация шифров

Введем формальное определение шифра и его составных частей. Пусть T, C и K — конечные множества возможных открытых текстов, шифртекстов и ключей. Обычно каждое из этих множеств представляет собой множество слов в некотором алфавите, причем алфавиты открытых текстов, шифртекстов и ключей могут различаться.

Для большинства современных систем шифрования открытые тексты, шифртексты и ключи представляют собой слова в алфавите {0,1}, т.е. последовательности нулей и единиц.

Процедура шифрования задает функцию Ek: T C, которая отображает множество открытых текстов во множество шифртекстов в зависимости от некоторого ключа k 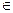K. Аналогично, процедура расшифрования Dk: C T также зависит от ключа k и отображает множество шифртекстов во множество открытых текстов. Так как получатель всегда должен иметь возможность по шифртексту восстановить исходный текст, то при любом k из K функции Ek и Dk должны удовлетворять условию:

Dk ° Ek =I, где I — тождественное отображение T в T.

Примечание 1. Во многих криптографических системах предполагается, что открытый текст, шифртекст и ключ — это целые числа. Такое предположение удобно для построения и обоснования алгоритмов шифрования и расшифрования, поскольку числовые функции хорошо изучены. Вместе с тем, это не ограничивает область применения таких алгоритмов, потому что любой текст, записанный с помощью букв, например, русского алфавита, всегда можно представить в виде целого числа. Обычно для этого каждый символ алфавита кодируют набором нулей и единиц (например, в соответствии с таблицей ASCII), и текст представляют в виде последовательности кодов соответствующих символов, записанных друг за другом. Получившаяся последовательность нулей и единиц является числовым представлением текста.

Примечание 2. Часто при реализации алгоритмов шифрования и расшифрования бывает удобно считать, что длина ключа, используемого для преобразования текста, равна длине самого текста или зависит от длины текста каким – то определенным образом. Очевидно, что если ключ используется для шифрования нескольких текстов, то его длина не может зависеть от длины каждого конкретного текста. В этом случае перед шифрованием текста поступают так: на

основе данного секретного ключа фиксированной длины с помощью определенного алгоритма формируют ключ шифрования, имеющий необходимую длину. Полученный ключ шифрования используют для преобразования текста. Простейшим способом сформировать ключ шифрования нужной длины является периодическое повторение символов секретного ключа. Например, из секретного ключа k = (k1, k2, …, k n) можно получить ключ шифрования (k1, k2, …, kn, k1, k2, …, kn, k1, k2, …, kn, k1…) произвольной длины.

Современные системы шифрования можно разделить на два больших класса:

• Симметричные (одноключевые) системы — в них для шифрования и расшифрования текста используется один и тот же ключ к.

• Асимметричные (двухключевые) системы используют различные ключи для шифрования и расшифрования текста.

Для таких систем ключ k можно представить в виде пары (ke, kd), где часть ke используется для шифрования, а kd — для расшифрования.

Дата добавления: 2014-01-11