
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Шифры замены
|
|
|
|
Простейшим из шифров замены является одноалфавитная подставновка, называемая также шифром простой замены.
Ключом такого шифра является взаимно однозначное отображение (подстановка) F алфавита открытого текста (X) в шифртекста (Y): F: X 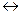 Y. Зафиксируем нумерацию символов в алфавитах X и Y: X = {
Y. Зафиксируем нумерацию символов в алфавитах X и Y: X = { 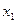 ,
,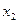 , …
, … 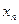 }, Y = {
}, Y = { 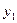 ,
, 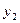 , …
, … 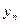 }.
}.
Тогда отображение F фактически задается перестановкой 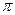 порядка n = |X | = |Y |: при шифровании символ xi открытого текста заменяется на символ
порядка n = |X | = |Y |: при шифровании символ xi открытого текста заменяется на символ 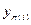 шифртекста.
шифртекста.
Эта перестановка может быть задана либо таблицей, либо с помощью формулы. При задании с помощью формулы значение 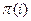 представляется в виде выражения, зависящего от i.
представляется в виде выражения, зависящего от i.
Пример. Типичным примером шифра замены является шифр Цезаря. Этот шифр реализует следующее преобразование текста, записанного с помощью латинского алфавита: каждая буква открытого текста заменяется буквой, стоящей на три позиции позже нее в алфавите (при этом алфавит считается записанным по кругу, то есть после буквы ‘z’ идет буква ‘a’).
Открытый текст ‘secret’ будет преобразован в ‘vhfuhw’. Ключ для шифра Цезаря можно задать в виде следующей таблицы (рис. 3). В первой строке записаны буквы открытого текста, во второй — соответствующие им буквы шифртекста.
 Рис. 3. Ключ для шифра Цезаря
Рис. 3. Ключ для шифра Цезаря
|
Шифр Цезаря можно описать и в виде формулы. Для этого пронумеруем буквы латинского алфавита числами от 0 до 25: a = 0, b = 1, …, z = 25. Тогда правило замены можно описать следующим образом: буква с номером i заменяется на букву с номером i+3 (mod 26), где операция ‘mod 26’ означает вычисление остатка от деления на 26.
Возможен обобщенный вариант шифра Цезаря, при котором буква с номером i заменяется на букву с номером i + k (mod 26). В этом случае ключом шифра является число k.
Еще больше обобщив этот метод, придем к семейству аффинных шифров. Для алфавита из n символов { 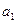 ,
, 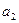 , …,
, …, 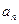 } аффинным шифром называется процедура, заменяющая входной символ
} аффинным шифром называется процедура, заменяющая входной символ 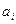 на символ
на символ 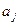 , где j = k · i + l (mod n).
, где j = k · i + l (mod n).
Шифры простой замены в настоящее время не используются, поскольку их стойкость невелика. Методы взлома таких шифров основаны на анализе частотности отдельных символов и их комбинаций. Дело в том, что в любом языке различные буквы и комбинации из двух, трех или большего количества букв имеют характерные частоты повторений в текстах. Например, в текстах на русском языке чаще всего встречается буква ‘О ’, затем, в порядке убывания частоты, идут буквы ‘Е ’ (считая, что ‘Е ’ и ‘Ё ’ — одна и та же буква), ‘А ’, ‘И ’,
‘Т’ и т. д. Для английского языка аналогичная последовательность самых частых букв: ‘E’, ‘T’, ‘A’, ‘I’, ‘N’. Самым частым символом в текстах является, однако, не буква, а символ пробела.
Становится ясно, что при использовании шифра простой замены частота повторений зашифрованных символов в шифртексте совпадает с частотой повторений соответствующих исходных символов в открытом тексте. Это позволяет достаточно легко вскрыть такой шифр. Более тонкие характеристики (учет сочетаемости различных букв) позволяют даже автоматизировать процесс взлома.
Для того чтобы увеличить стойкость шифров замены, применяют многоалфавитную замену.
Процедура шифрования для многоалфавитной замены включает набор подстановок {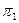 ,
, 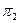 , …,
, …, 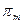 } и функцию - распределитель
} и функцию - распределитель 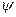 (k, i), задающую последовательность применения подстановок
(k, i), задающую последовательность применения подстановок 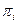 .
.
При шифровании i-го символа открытого текста применяется подстановка с номером 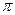 (k,i), где k — ключ шифрования.
(k,i), где k — ключ шифрования.
Частным случаем многоалфавитной замены является шифр Виженера. Формально этот шифр можно описать следующим образом.
В качестве ключа шифрования выберем набор из m целых чисел:
k = ( 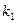 ,
, 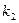 , …,
, …, 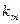 ). Процедуру преобразования открытого текста t = (
). Процедуру преобразования открытого текста t = ( 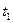 ,
, 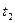 , …) в шифртекст c = (
, …) в шифртекст c = ( 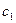 ,
, 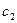 , …) построим на основе обобщенного шифра Цезаря:
, …) построим на основе обобщенного шифра Цезаря:
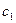 =
= 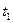 +
+ 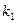 (mod 26),
(mod 26), 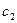 =
= 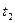 +
+ 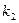 (mod 26), и т.д. Когда будут использованы все m компонент ключа k, для шифрования (m+1) -й буквы снова возьмем
(mod 26), и т.д. Когда будут использованы все m компонент ключа k, для шифрования (m+1) -й буквы снова возьмем 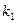 , и т.д. Фактически, в качестве ключа шифрования используется бесконечная последовательность, образованная периодическим повторением исходного набора:
, и т.д. Фактически, в качестве ключа шифрования используется бесконечная последовательность, образованная периодическим повторением исходного набора: 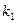 ,
, 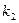 , …,
, …, 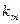 ,
, 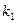 ,
, 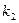 , …,
, …, 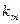 ,
, 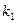 ,
, 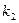 , … Такую последовательность принято называть гаммой.
, … Такую последовательность принято называть гаммой.
Взломать шифр многоалфавитной замены немного сложнее, чем шифры простой замены, но тоже достаточно легко. Такой шифр на самом деле представляет собой одновременное применение m шифров простой замены (обобщенный шифр Цезаря), причем часть исходного текста, состоящая из букв  ,
, 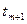 ,
, 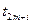 , … шифруются с использованием «ключа» ki (i=1, …, m).
, … шифруются с использованием «ключа» ki (i=1, …, m).
Если известен период гаммы (т.е. число m), то к каждой такой части можно применить любой из методов взлома шифров простой замены. Если период гаммы не известен, то задача усложняется. Но и для этих случаев разработаны эффективные методы взлома. Эти методы позволяют с достаточной вероятностью определить период гаммы, после чего задача сводится к взлому шифра гаммирования с известным периодом.
Как было указано выше, основой для атак на шифры замены является анализ частот вхождений символов в шифртекст. Для того чтобы затруднить взлом шифра замены, можно попытаться скрыть частотные свойства исходного текста. Для необходимо, чтобы частоты появления разных символов тексте совпадали.
Такие шифры замены называются гомофоническими.
Простейшим вариантом гомофонического шифра является следующий. Предположим, что нам известны частоты вхождений символов в открытый текст. Пусть fi — частота появления i–го символа в открытом текста (i — номер буквы в алфавите). Каждой  исходного алфавита (т.е. алфавита, с помощью которого записывается открытое сообщение) сопоставим подмножество
исходного алфавита (т.е. алфавита, с помощью которого записывается открытое сообщение) сопоставим подмножество  , содержащее
, содержащее 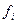 символов выходного алфавита (т.е. алфавита, с помощью которого записывается шифртекст). Причем никакие два подмножества
символов выходного алфавита (т.е. алфавита, с помощью которого записывается шифртекст). Причем никакие два подмножества  и
и 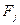 не пересекаются. При шифровании будем заменять каждое вхождение символа
не пересекаются. При шифровании будем заменять каждое вхождение символа  на случайный символ из множества
на случайный символ из множества  .
.
Очевидно, что средняя частота появления в шифртексте любого из символов выходного алфавита одинакова, что существенно затрудняет криптоанализ.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1063; Нарушение авторских прав?; Мы поможем в написании вашей работы!