Решение систем линейных алгебраических уравнений

2.1. Постановка задачи

Требуется найти решение системы линейных уравнений:

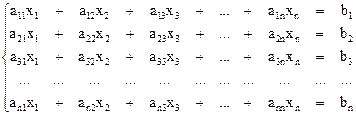
или в матричной форм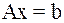е: , где

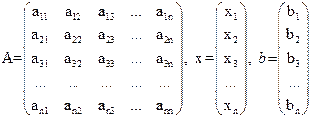
По правилу Крамера система 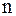линейных уравнений имеет единственное решение, если определитель системы отличен от нуля 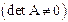и значение каждого из неизвестных определяется следующим образом: 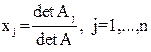, где 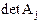– определитель матрицы, получаемой заме-

ной 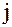-го столбца матрицы 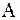столбцом правых частей .

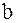Непосредственный расчет определителей для больших 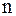является очень трудоемким.

Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций.

Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших 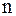требуется большое количество операций, и возникает опасность накопления погрешностей.

Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов.

Норма матрицы является некоторой обобщенной оценкой значений элементов матрицы. Для её вычисления можно использовать следующие выражения:

,

, .

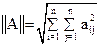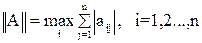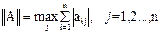2.2. Метод простой итерации

Для того чтобы применить метод простой итерации, необходимо систему уравнений

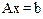(1)

с квадратной невырожденной матрицей 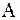привести к виду

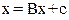, (2)

где 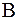– квадратная невырожденная матрица с элементами ,
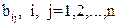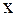– вектор-столбец неизвестных 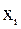, 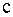– вектор-столбец с элементами 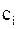, 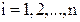. Существуют различные способы приведения системы (1) к виду (2). Рассмотрим самый простой.

Представим систему в развернутом виде:

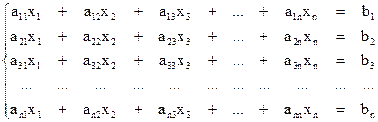(3)

Из первого уравнения системы (3) выразим неизвестную :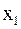

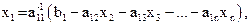из второго уравнения – неизвестную :

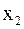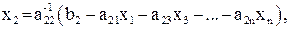и т. д. В результате получим систему:

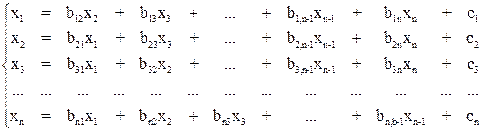(4)

Матричная запись системы (4) имеет вид (2). На главной диагонали матрицы 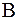находятся нулевые элементы, а остальные элементы вычисляются по формулам:

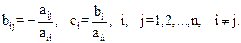(5)

Очевидно, что диагональные элементы матрицы 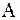должны быть отличны от нуля. Выберем произвольно начальное приближение. Обычно в качестве первого приближения берут 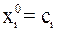или 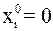. Подставим начальное приближение в правую часть (4). Вычисляя левые части, получим значения 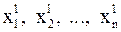. Продолжая этот процесс дальше, получим последовательность приближений, причем 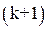приближение строится следующим образом:

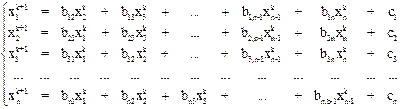
Последняя система представляет собой расчетные формулы метода простой итерации.

Сходимость метода простой итерации. Известно следующее достаточное условие сходимости метода простой итерации.

Если элементы матрицы 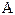удовлетворяют условию:

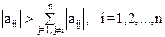, (6)

то итерационная последовательность 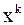сходится к точному решению 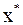.Условие (7) называют условием преобладания диагональных элементов матрицы 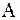, так как оно означает, что модуль диагонального элемента 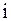-ой строки больше суммы модулей остальных элементов этой строки, .

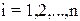Необходимо помнить, что условие сходимости (6) является лишь достаточным. Его выполнение гарантирует сходимость метода простых итераций, но его невыполнение, вообще говоря, не означает, что метод расходится.

Справедлива следующая оценка погрешности:

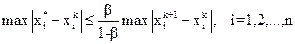, (7)

где 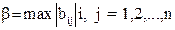. Правую часть оценки (7) легко вычислить после нахождения очередного приближения.Иначе достаточное условие (6) для матрицы 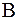может быть переформулирована так: если 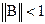, то итерационный процесс (6) сходится к точному решению системы.

Критерий окончания. Если требуется найти решение с точностью 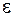, то в силу (7) итерационный процесс следует закончить, как только на 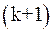-ом шаге выполнится неравенство: .

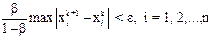Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство 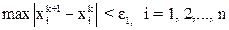, где .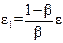

Если выполняется условие 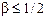, то можно пользоваться более простым критерием окончания:

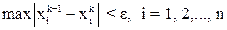. (8)

В других случаях использование последнего критерия (8) неправомерно и может привести к преждевременному окончанию итерационного процесса.

Дата добавления: 2014-01-11