Метод Зейделя

.

Модификацией метода простой итерации можно считать метод Зейделя.

В методе простой итерации на 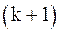-ой итерации значения 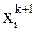, 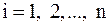вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении 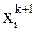используются значения 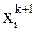, , , 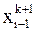уже найденные на 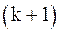-ой итерации, а не 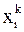, , 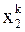…, , 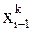как в методе простой итерации, т.е. 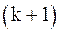-е приближение строится следующим образом:

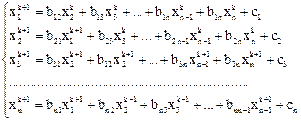(9)

Эти формулы являются расчетными формулами метода Зейделя.

Введем нижнюю и верхнюю треугольные матрицы:

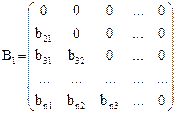и .

Матричная запись расчетных формул (9) имеет вид: . Так как 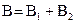, точное решение 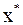исходной системы удовлетворяет равенству: .

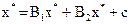Сходимость метода Зейделя. Достаточным условием сходимости метода Зейделя является выполнение неравенства:

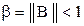. (10)

Неравенство (10) означает, что для сходимости метода Зейделя достаточно, чтобы любая норма матрицы 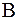был меньше единицы.

Если выполнено условие (10), то справедлива следующая оценка погрешности:

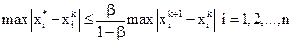, (11)

где 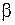– норма матрицы.

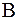Критерий окончания. Если требуется найти решение с точностью 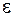, итерационный процесс следует закончить, как только на 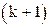-ом шаге выполнится неравенство: 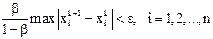. Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство , где 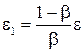. Если выполняется условие

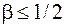, то можно пользоваться более простым критерием окончания:

.

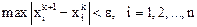Метод Зейделя, как правило, сходится быстрее, чем метод простой итерации. Однако возможны ситуации, когда метод простой итерации сходится, а метод Зейделя сходится медленнее или вообще расходится.

Пример. Применим метод Зейделя для решения системы уравнений из предыдущего примера. Первые шаги полностью совпадают с процедурой решения по методу простых итераций. Проведем теперь итерации методом Зейделя.

При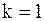

.

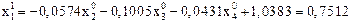При вычислении 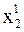используем уже полученное значение :

.

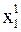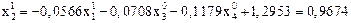При вычислении 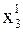используем уже полученные значения и :

.

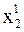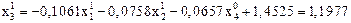При вычислении 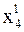используем уже полученные значения , , :

.

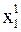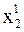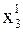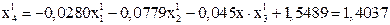Аналогичным образом проведем вычисления пр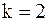и и .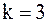

Получим:

при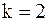

.

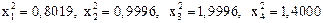при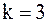

.

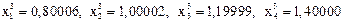Известны точные значения переменных:

.

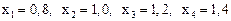Сравнение с предыдущим примером показывает, что метод Зейделя сходится быстрее и дает более точный результат.

Дата добавления: 2014-01-11