Многочлен Ньютона с конечными разностями

Рассмотрим случай равноотстоящих узлов интерполяции, т. е. 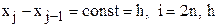– называется шагом.

Введем понятие конечных разностей. Пусть известны значения функции в узлах . Составим разности значений функции:

Эти разности называются разностями первого порядка.

Можно составить разности второго порядка:

.

Аналогично составляются разности k-го порядка:

.

Выразим конечные разности непосредственно через значение функции:

Таким образом, для любого k можно записать:

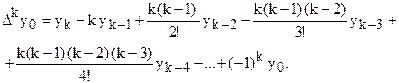
Запишем эту формулу для значений разности в узле :

.

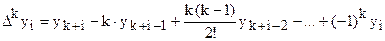Используя конечные разности, можно определить

.

Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде

.

График многочлена должен проходить через заданные узлы, то есть . Используем эти условия для нахождения коэффициентов многочлена:

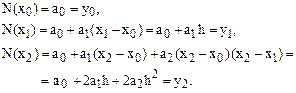
Найдем отсюда коэффициенты :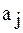

Таким образом, для любого -го коэффициента формула примет вид

.

Подставляя эти формулы в выражение многочлена Ньютона, получим его следующий вид:

Полученную формулу можно записать в другом виде. Для этого введем переменную .

В этом случае

С учетом этих соотношений формулу многочлена Ньютона можно записать в виде

.

Полученное выражение может аппроксимировать данную функцию 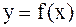на всем отрезке изменения аргумента . Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем , то есть использовать эту формулу для всех . Для других случаев вместо принять , если при . В этом случае интерполяционный многочлен можно записать в виде

Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед. Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Это объясняется следующим: разности вычисляются через значения функции , причем . Из-за этого при больших значениях 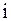мы не можем вычислить высших порядков .

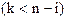Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае , то есть 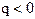, и интерполяционный многочлен Ньютона можно получить в виде:

.

Полученная формула называется вторым интерполяционным многочленом назад.

Пример. Используя интерполяционный полином Ньютона, вычислить 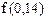, где функция 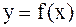задана таблицей

х		0,1	0,2	0,3	0,4	0,5
у		0,1002	0,2013	0,8045	0,4108	0,5211

Решение. Составляем таблицу конечных разностей.

х	у
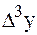
		0,1002
0,1	0,1002		0,0009
		0,1011		0,0012
0,2	0,2013		0,0021		-0,0002
		0,1032		0,0010		0,0001
0,3	0,3045		0,0031		-0,0001
		0,1063		0,0009
0,4	0,4108		0,0040
		0,1103
0,5	0,5211

Для вычисления положим в интерполяционном многочлене Ньютона вперед 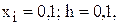тогда и

Пример. Задана таблица. Найти .

х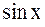
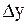
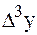
	0,2588
		0,0832
	0,3420		-0,026
		0,0806		0,0006
	0,4226		-0,032
		0,0774		0,0006
	0,5		0,038
		0,0736
	0,5736

При вычислении положим

.

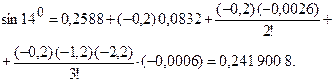
При вычислении положим

.

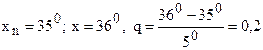Оценим погрешности формул Ньютона вперед и назад:

где и

где .

Формулы приближенного дифференцирования основаны на первой интерполяционной формуле Ньютона. Интерполяционный многочлен Ньютона имеет вид

,

где

Производя перемножение биномов, получим

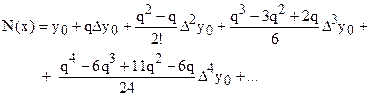
так как 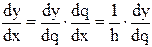, то

.

Аналогично можно вычислять производные функции любого порядка.

В некоторых случаях требуется находить производные функций 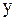в основных табличных точках . Так как табличное значение можно считать за начальное, то положив , имеем

,

Для производной многочлена Ньютона первого порядка погрешность может быть вычислена по формуле ,

где – число конечных разностей в многочлене Ньютона.

Пример. Найти 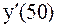функции , заданной таблично.

Дата добавления: 2014-01-11