Лекция №2. Постулаты квантовой механики

Постулаты квантовой механики

Исторически квантовая механика строилась на постулатах, которые не имели объяснения на момент их введения, но, следуя им, ученые добивались хорошего соответствия расчетных и экспериментальных характеристик квантовых явлений. Например, Планк постулировал, что излучение атомов дискретно и наименьшая порция энергии излучения 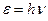, что позволило разрешить проблему спектра излучения абсолютно черного тела («ультрафиолетовая катастрофа»). А Нильс Бор постулировал существование стационарных (неизлучающих) орбит электронов в атоме, что позволило точно рассчитать спектр водорода и постоянную Ридберга. Но с развитием квантовой механики эти постулаты получили свое объяснение.

Однако сам формализм квантовой механики не имеет строгого (в математическом смысле) обоснования, и основан на формальных постулатах. Но, разумеется, к формулировке этих постулатов физики пришли в результате обобщения экспериментальных данных и анализа соответствия им создаваемых методов математического описания квантовых процессов.

Для того, чтобы сформулировать эти постулаты сначала введем некоторые основные понятия функционального анализа, оперирующего в пространстве функций, вообще говоря, комплексных.

Пусть 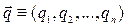– набор обобщенных координат, например, координат и скоростей частицы, или, как еще говорят, вектор в конфигурационном пространстве Q.

Определение

Скалярным произведением функций j( 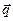) и y( 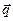) называется интеграл

.

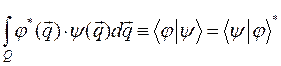Следствие

Если 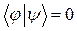, то говорят, что j и ψ ортогональны.

Пример. Пусть 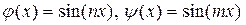. Рассмотрим их скалярное произведение на интервале [-π, π]:

,

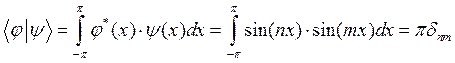то есть эти функции ортогональны на интервале [-π, π] при n ≠ m.

В новых обозначениях полученные ранее соотношения можно записать в виде:

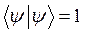- условие нормировки на 1,

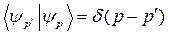- условие нормировки на δ- функцию,

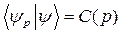- амплитуда вероятности,

Определение.

Оператором называется математический объект (обозначаемый «крышкой» над буквой, например, 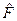), действующий на функцию, а результатом этого действия является другая функция, т.е.

.

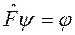Примером операторов могут служить, в частности, операторы дифференцирования и интегрирования:

.

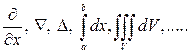Пример. а) Пусть 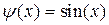, тогда действие интегрального оператора определяется соотношением:

.

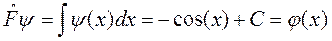б) Рассмотрим дифференциальный оператор. Пусть 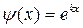, тогда

.

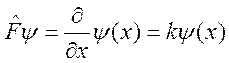Определение. Если функция y удовлетворяет уравнению

,

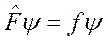где f – действительное число, то такая функция называется собственной функцией оператора 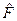, а число f - собственным числом оператора .

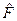Скалярное произведение с оператором обозначается следующим образом:

.

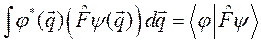
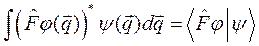Часто в физической литературе можно встретить и другие обозначения:

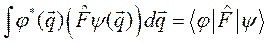
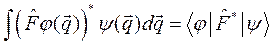
В таких обозначениях оператор 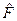действует на функцию, стоящую справа, а комплексносопряженный оператор 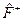действует на функцию, стоящую слева.

Определение

Оператор 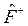называется эрмитово сопряженным к 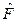на множестве функций W, если

.

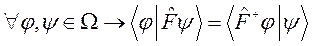Пример. Пусть оператор 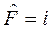, то есть его действие заключается в умножении функции на мнимую единицу. Тогда 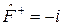и на основании соотношения

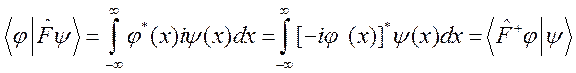
оператор 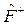является эрмитово сопряженным к .

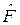Определение

Если 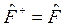, то оператор 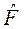называется самосопряженным или

эрмитовым оператором.

Следствие

Эрмитов оператор удовлетворяет соотношению

,

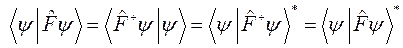которое показывает, что скалярное произведение 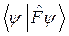– действительно, т.е. можно записать

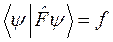, (2.1)

где f – действительное число.

Пример. Пусть оператор 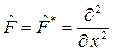, а функцию возьмем в виде 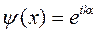, тогда на этом классе функций

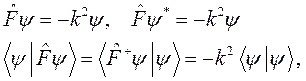
то есть такой оператор является самосопряженным (эрмитовым).

Теперь перейдем к формулировке постулатов квантовой механики.

Первый постулат квантовой механики был упомянут ранее и определяет смысл волновой функции, а именно:

Квантовая система полностью описывается волновой функцией y( 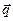), а величина

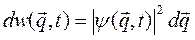
есть вероятность обнаружить частицу в элементе объема конфигурационного пространства 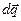, расположенного в точке, определенной вектором .

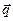Второй постулат квантовой механики есть формулировка принципа суперпозиции для волновых функций, а именно:

Если y₁ – волновая функция состояния 1, а y₂ – волновая функция состояния 2, то их линейная комбинация y₃ = с₁y₁ + с₂y₂ описывает либо состояние 1, либо состояние 2.

Как нетрудно заметить, квантовый принцип суперпозиции отличается от классического, проявляющегося, например, при интерференции волн. Рассмотрим для примера образование молекул водорода и хлористого водорода.

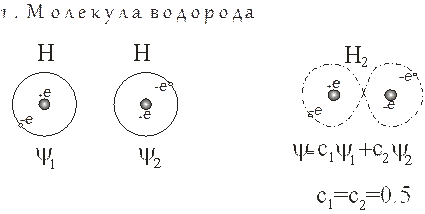
При образовании молекулы водорода вероятность каждому из двух электронов находиться около какого-нибудь ядра одинакова и равна 0.5.

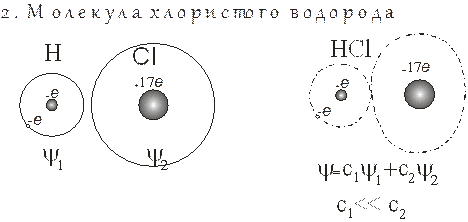
В молекуле хлористого водорода вероятность электрону, взятому у водорода, находиться около иона хлора значительно больше, то есть с₁«с₂.

Третий постулат квантовой механики (принцип соответствия):

Каждой физической величине F в квантово-механическом описании соответствует линейный эрмитовый оператор 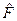, собственные значения которого равны измерениям величины F в состояниях, описываемых волновой функцией 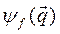, являющейся собственной функцией оператора 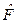, т.е.

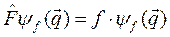(2.2)

Определение.

Собственное значение f называется квантовым числом оператора .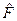

Следствие

Поскольку измерение величины F обязательно дает одно из собственных значений, то любая волновая функция в случае дискретного набора (спектра) собственных значений f может быть представлена в виде суперпозиции всех состояний

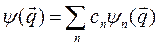, (2.3)

а в случае непрерывного спектра

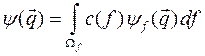. (2.4)

Если система допускает и дискретный и непрерывный спектр, то

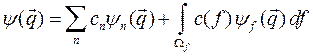. (2.5)

Четвертый постулат квантовой механики:

В случае дискретного спектра измерение F дает значение f_n с вероятностью 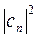, а в случае непрерывного спектра измерение F дает значение в интервале (f, f+df) с вероятностью .

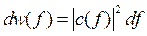Условие нормировки в общем случае имеет вид:

.

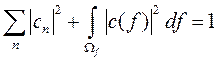Величины c_n и c(f) называются амплитудами вероятности.

Следствием этих постулатов являются следующие полезные соотношения:

– выражения для амплитуд вероятности

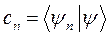(2.6а)

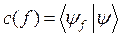(2.6б)

– условия нормировки

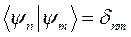(2.6в)

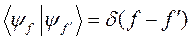(2.6г)

Дата добавления: 2014-01-11