Линеаризация уравнений статики

В большинстве случаев для реальных звеньев автоматической системы связь между значениями выходной и входной координатами является нелинейной. Поэтому и уравнения статики, и уравнения динамики системы в целом, как правило, получаются нелинейными. Нелинейные дифференциальные уравнения вносят значительные затруднения в решение задач, особенно в тех случаях, когда они имеют высокий порядок. Поэтому очень часто стараются заменить в первом приближении нелинейное дифференциальное уравнение или уравнение статики линейными, анализ которых выполняется значительно проще.

Такая замена нелинейных зависимостей линейными называется линеаризацией. Полученные в результате линеаризации приближенные уравнения могут быть положены в основу приближенного исследования достаточно широкого класса систем автоматического регулирования непрерывного действия. Выводы, получаемые в линейной теории автоматического регулирования, основанные на исследовании линеаризованных систем, имеют большое практическое значение.

Рассмотрим физическую сущность метода линеаризации на примере АСР температуры нагревательной печи. Для измерения температуры в печи используется платинородий-платиновый термоэлектрический термометр, статическая характеристика которого приведена на рисунке 2.6.

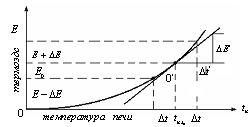
Рисунок 2.6– К вопросу линеаризации нелинейных характеристик.

При отклонении регулируемой температуры от заданного значения , называемого также номинальным, (например, в результате повышения теплоотдачи печи во время ее загрузки деталями, подлежащими нагреву) произойдет изменение тэдс на величину ∆Е.

Однако в замкнутой АСР регулятор будет воздействовать на источник тепла таким образом, чтобы температура в печи приняла заданное значение. Поэтому отклонения температуры, а следовательно, и величины тэдс от номинальных значений будут незначительны.

Учитывая малость отклонений, можно в окрестностях точки 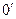, соответствующей равновесному состоянию, заменить участок кривой прямой, касательной к этой кривой в точке .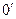

При такой замене получаем линейную зависимость между тэдс и температурой около равновесного состояния:

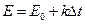(2.10)

В уравнении (2.10) коэффициент 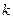может быть определен из графика (рис. 2.6).

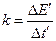(2.11)

Если перенесем начало координат в точку равновесного состояния, получим более простую зависимость.

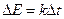(2.12)

где .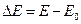

Если зависимость между выходной и входной координатами задана аналитически, то линеаризация осуществляется с помощью разложения функции в ряд Тейлора в окрестности точки, характеризующей состояние равновесия. В этом разложении оставляют только отклонения первой степени.

Допустим, что уравнение нелинейного звена имеет вид:

(2.13)

Запишем разложение этой функции в ряд Тейлора для точки равновесного состояния А :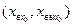

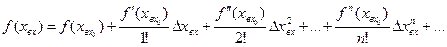(2.14)

Отбрасывая из ряда члены высших порядков малости, т.е. содержащие отклонения координаты 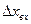в степенях выше первой, получим:

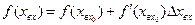(2.15)

Учитывая, что 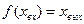, , 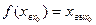, 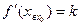получим:

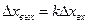(2.16)

Выражение (2.16) и представляет собой линеаризованную функцию 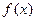, представленную в отклонениях от равновесного состояния. Производная 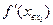этой функции в точке равновесного состояния равна тангенсу угла наклона линеаризованного участка в окрестности точки равновесного состояния.

Рассмотрим конкретный пример. Уравнение статики имеет вид:

(2.17)

Необходимо линеаризовать эту зависимость в окрестности точки равновесного состояния .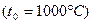

Искомое уравнение должно иметь вид:

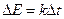(2.18)

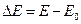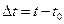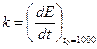, , (2.19)

Определяем

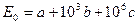(2.20)

Определяем

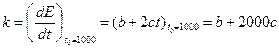(2.21)

Искомое уравнение имеет вид:

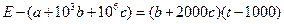(2.22)

Или

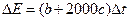(2.22)

Следует отметить, что статические характеристики экстремальных и релейных звеньев линеаризации не поддаются. Поэтому такие характеристики называют существенно нелинейными.

Дата добавления: 2014-01-11