Вычисление ДВИ в декартовых координатах

Основные свойства ДВИ

Сравнивая определения ДВИ и ОИ можно сделать вывод, что принципиально они не отличаются, поэтому и их свойства будут аналогичными.

1.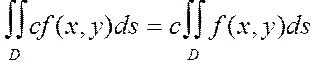 с=const

2.

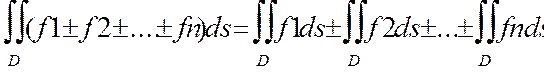
3. Если область Д разбить на 2 части Д1 и Д2, такие что Д1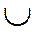Д2=Д, то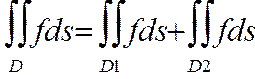

4.

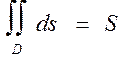
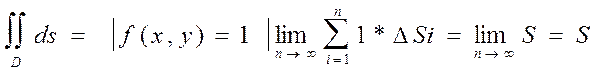
Пусть область интегрирования ограничена двумя непрерывными кривыми(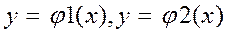) двумя прямыми (x=a,x=b), причем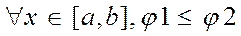

Такая область Ду наз. правильной в направлении оси ОУ.

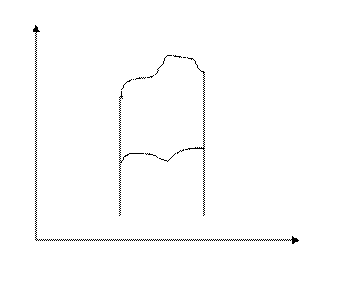
любая прямая, проходящая через любую точку М области Ду пересекает границу области только в 2 точках.

Пусть область интегрирования ограничена двумя непрерывными кривыми 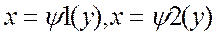и двумя прямыми у=с и y=d, причем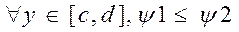

Такая область Дх наз. правильной в направлении оси ОХ.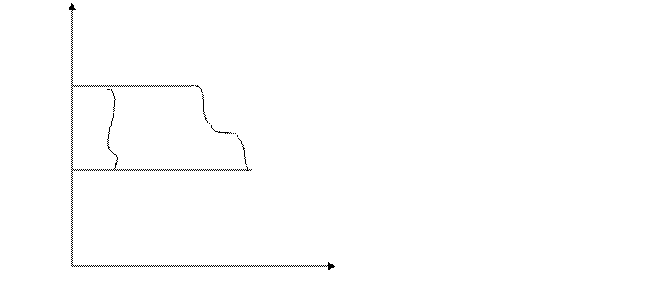

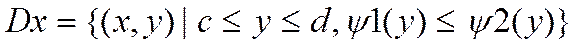
причем любая прямая проходящая через внутреннюю точку М пересекает границу этой области только в двух точках.

Область Ду(Дх) представляет собой разность двух криволинейных трапеций с одним и тем же основанием на оси ОХ(ОУ).

Теорема2: (о сведении ДВИ к повторному интегралу) ДВИ по области Ду можно вычислить сведением к ОИ по переменной х от ОИ по переменной у, по формуле:

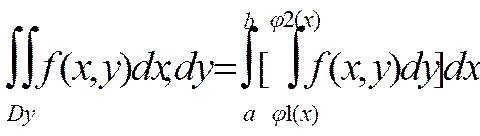(6)

ДВИ по области Дх можно вычислить сведением к ОИ по переменной у от ОИ по переменной х.

(7)

Доказательство:

Рассмотрим доказательство этой теоремы для случая, когда область интегрирования есть Ду, т.е. правильная в направлении оси ОУ. А функция Z=f(x,y)=>0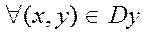

Рассмотрим цилиндрическое тело ограниченное сверху поверхностью Z=f(x,y), снизу областью Ду, и боковой цилиндрической поверхностью, с образующей параллельной оси z и направляющей границы Ду.

Согласно геометрическому смыслу ДВИ объем этого ц.т. определяется формулой:

Vц.т.= 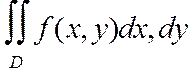(8)

С другой стороны, при изучении геометрических приложений ОИ было показано что если известны площади поперечных сечений S(x) тела плоскостями перпендикулярными оси ОХ, то объем эжтого тела определяется формулой:

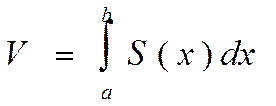(9), где

S(x)-непрерывная функция, которая для каждого фиксированного х выражает площадь поперечного сечения тела плоскотью перпендикулярной оси Х.

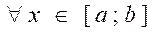
Построим сечение этого Ц.Т. плоскостью Х=Х0, перпендикулярной оси.

В сечении получим криволинейную трапецию MNPQ, которая ограничена сверху кривой z=f(X0,Y) слева и справа вертикальными отрезками MQ и NP, а снизу отрезком MN, причем М(Х0,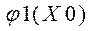),N(X0,).

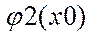Площадь этой криволинейной трапеции можно найти с помощью ОИ.

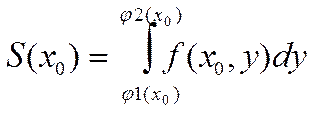(10)

имеем

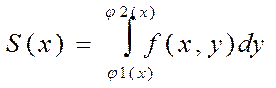(11)

Подставим (11) в (9)

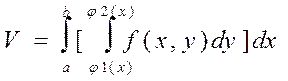(12)

Сопоставляя формулы (8) и (12) окончательно получим:

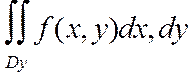
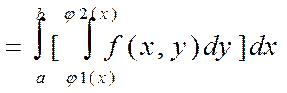
В случае если область интегрирования есть Дх рассекая это Ц.т. плоскостью У=У0, аналогично получим:

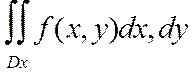
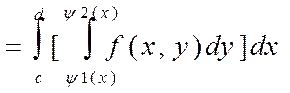
Замечания:

1.Если область Д правильная в обоих направлениях, то можно применять любую из формул (6) или (7)

2. Если область Д не является правильной ни по х ни по у, то ее нужно разбить на правильные подобласти прямыми параллельными осям координат.

3. Формулы (6) и (7) остаются в силе когда никакие ограничения на функцию Z=f(x,y) не накладываются.

Интегралы, стоящие в правых частях формул (6) и (7) наз. повторными интегралами. Интегралы в квадратных скобках – внутренними. А интегралы от них - внешними.

Внешний интеграл всегда имеет постоянные пределы интегрирования и берется после вычисления внутреннего.

При вычислении внутреннего интеграла переменная не совпадающая с переменной интегрирования считается постоянной величиной.

Дата добавления: 2014-01-11