Скалярное поле

Рассм. СП задаваемое скалярной ф-цией U=U(x,y,z) (U=U(x,y)) для наглядного изобр.СП применяют поверхности(линии) уровня.

Опр.3 Поверхностью (линии) уровня СП определяемого ф-цией U(x,y,z) (U(x,y)), наз. геометр. место точек в которых рассматриваемая ф-ция принимает постоянное значение. Уравнения поверхности (линии уровня) имеют вид U(x,y,z)=с (U(x,y)=с), где с-const.

Пример

Найти ур-я поверхностей уровня, СП определяемой ф-цией U=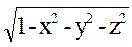, U(x,y,z)=c==> U=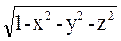=c

|c|<=1 1-x²-y²-z² = c²

x²+y²+z² =1- c² т.о. поверхностями уровня заданной ф-ции явл. семейство концентрических сфер с центром в начале координат.

Покажем, что всякое СП порождает некоторое векторное.

Из теор. Ф-ций нескольких переменных известно, что градиентом ф-ции U(x,y,z) (скалярного поля U(x,y,z)) в т.М наз. вектор корд. Которого являются значения ЧП(частных производных) заданной ф-ции в рассматриваемой точке.

Дельта-(δ)

grad U=(, , )= + +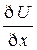

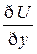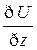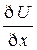
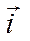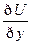
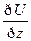
Также известно, что производная т. U, по заданному направлению ℓ определяемому формулой:

ℓ=l

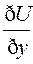= cos α+cosβ + 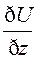cosγ, (2)

cos α, cosβ, cosγ -направление cos направление ℓ.

Производная по направлению характеризует скорость изменения ф-ции в точке в заданном направлении ℓ:

если 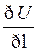>0, тогда ф-ция (СП) в зад. направлении ↑

<0, то ф-ция U в задан.направлении. ↓

Пусть ℓ⁰ - единичный вектор заданный направл.ℓ, тогда

ℓ⁰= (cos α, cosβ, cosγ)

Тогда формулу (2) можно записать:

=grad U *ℓ⁰ =|grad|*|ℓ⁰ |*(cos gradU,ℓ⁰)=|grad|*cosφ (3)

Из формулы (3) видно, что 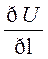достигает своего наибольшего значения когда cosφ равен 1 (φ=0), иными словами произв. достигает своего наибольшего значения когда направление вектора grad совпадает с направлением дифференцирования, и это наибольшее

Равно:

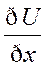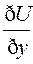max =|grad U|= корень из след. выражения ()²+(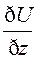)² + ()²

Т.о. grad СП U указывает направление наибольшего возрастания ф-ции (поля). Всякое СП U(M) порождает ВП grad U(M)

grad- векторная характеристика скалярного поля.

Осн. Свойства:

1)grad ф-ции в каждой точке ┴ линии (поверхности) уровня проходящей через заданную точку.

2) grad(U±V)= grad U ± grad V

3) grad(c*V)= c grad,c - const

4) grad (U*V)=grad U*V+ UgradV

5)grad (U/V)=(gradU*V-UgradV)/V²

6)grad(f(U))=f 'U*gradU

Каждое из этих свойств доказано на основании определения grad/

Доказательство 2)grad(U+V)=gradU+gradV

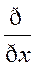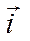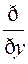grad(U+V)= (U+V) +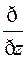(U+V) +(U+V) =

(+)+(+)+(+)

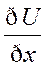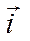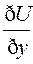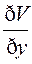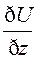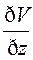Лк 13. ВЕКТОРНОЕ ПОЛЕ (ВП) и его характеристики.

Дата добавления: 2014-01-11