Случайные величины и законы их распределения

Случайной величиной называют такую неизвестную величину, которая в результате опыта может принять то или иное значение, при чем заранее неизвестно какое.

Обозначаются случайные величины Х, а возможные ее значения х

Случайные величины бывают дискретные и непрерывные

Случайная величина Х называется дискретной случайной величиной, если множество ее значений представляют собой конечную или бесконечную числовую последовательность и все значения дискретной случайной величины счетны.

Пример:

Производится 5 выстрелов. Найти вероятность того, что стрелок израсходует патроны, если он стреляет до одного попадания.

Решение:

Случайная величина Х- количество израсходованных патронов – это дискретная случайная величина. В данной ситуации она может принимать значения: 1,2,3,4,5

Случайная величина Х называется непрерывной случайной величиной, если множество ее значений, непрерывно заполняет некоторый промежуток

Пример:

Некоторый измерительный прибор имеет погрешность при каждом измерении от 0 до 0,1 ед. Найти вероятность того, какова погрешность измерения при каждом из десяти независимых опытов.

Решение:

Случайная величина Х – погрешность измерения при одном опыте – это непрерывная случайная величина.

ВАЖНО:

Задать случайную величину значит установить закон распределения случайной величины.

Законом распределения случайной величины называется соотношение, устанавливающее взаимосвязь между возможными значениями случайной величины и соответствующими им вероятностями.

Для дискретной случайной величины возможно установить 3 закона распределения:

1. Ряд распределения
2. Многоугольник распределения
3. Функция распределения

1. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены все возможные значения случайной величины и соотносящие им вероятности

			......
			......

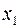
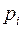
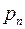
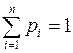
Пример:

Составить ряд распределения случайной величины исходя из условий: производится 3 независимых выстрела по мишени, вероятность попадания в каждом выстреле 0,6. Составить ряд числа попаданий.

Решение:

Х – число попаданий

	0,064	0,288	0,432	0,216

p(x=0)=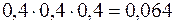

p(x=1)=

p(x=2)=

p(x=3)=

2. Многоугольником распределения называют ломаную линию с вершинами в точках(;); (;),... (;)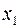

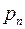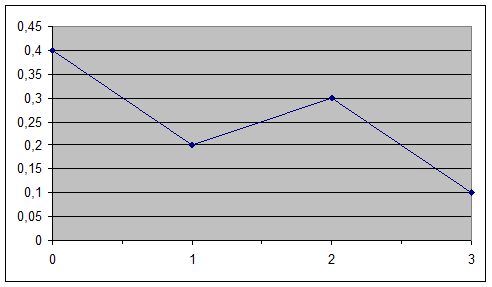
Пример: Построить многоугольник распределения дискретной случайной величины

Решение:

	0,4	0,2	0,3	0,1

3.Функцией распределения дискретной случайной величины называется вероятность того, что х примет значения меньшее данного.

F (X)= p(X<x)

Свойство функции распределения

1. Функция распределения- величина неубывающая
2. Все возможные значения функции распределения принадлежат [0;1]
3. F(-) =0

F(+) =1

1. p(a<х<в)= F(в)- F(а)

Вероятность того, что значение случайной величины будут принадлежать промежутку от а до в равняется, нужно из функции распределения значения в вычесть функцию распределения значения а

Графиком функции распределения дискретной случайной величины является ступенчатая ломанная линия.

Для данного ряда распределения построить функцию распределения

	0,1	0,2	0,3	0,1	0,3

F(-) =0

F(1) =p(X<1)=0

F(2) =p(X<2)=p(x=1)=0,1

F(3) =p(X<3)=p(x=1)+p(x=2)=0,1+0,2=0,3

F(4) =p(X<4)=p(x=1)+p(x=2)+p(x=3)=0

F(5) =p(X<5)=p(x=1)+p(x=2)+p(x=3)+p(x=4)=0,1+0,2+0,3+0,1=0,7

F(+) =p(X<+)=p(x=1)+ p(x=2)+p(x=3)+p(x=4)+p(x=5)=0,1+0,2+0,3+0,1+0,3=1

Построим функцию распределения

(схематично)

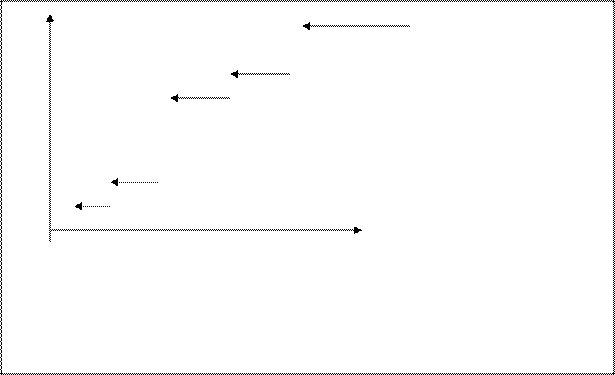
Дата добавления: 2014-01-11