Общая интерпретация реляционных операций

Реляционная алгебра

Кодд определяет так называемую "начальную" алгебру, т.е. набор из восьми операторов, символически показанный на рис.1. Однако важно понимать, что алгебра этими восемью операторами не исчерпывается. На самом деле можно было бы определить любое число операторов, которые удовлетворяли бы простому необходимому условию: "отношение на входе — отношение на выходе".

Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, то средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для баз данных.

Существует много подходов к определению реляционной алгебры, которые различаются набором операций и способами их интерпретации, но в принципе, более или менее равносильны. Мы опишем немного расширенный начальный вариант алгебры, который был предложен Коддом. В этом варианте набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса - теоретико-множественные операции и специальные реляционные операции. В состав теоретико-множественных операций входят операции:

• объединения отношений;
• пересечения отношений;
• взятия разности отношений;
• прямого произведения отношений.

Специальные реляционные операции включают:

• ограничение (выборка) отношения;
• проекцию отношения;
• соединение отношений;
• деление отношений.

Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения.

Реляционная алгебра в том виде, в котором она была определена Коддом, состоит из восьми операторов, составляющих две группы по четыре оператора.

1. Традиционные операции над множествами: объединение, пересечение, разность и декартово произведение (все они модифицированы с учетом того, что их операндами являются отношения, а не произвольные множества).

2. Специальные реляционные операции: выборка, проекция, соединение и деление.

Ниже приведены упрощенные определения этих восьми операторов (рис. 6.1).

Выборка Возвращает отношение, содержащее все кортежи из заданного отношения, которые удовлетворяют указанным условиям. Операцию выборки также иногда называют операцией ограничения.

Проекция Возвращает отношение, содержащее все кортежи (подкортежи) заданного отношения, которые остались в этом отношении после исключения из него некоторых атрибутов.

Произведение Возвращает отношение, содержащее все возможные кортежи, которые являются сочетанием двух кортежей, принадлежащих соответственно двум заданным отношениям.

Объединение Возвращает отношение, содержащее все кортежи, которые принадлежат либо одному из двух заданных отношений, либо им обоим.

Пересечение Возвращает отношение, содержащее все кортежи, которые принадлежат одновременно двум заданным отношениям.

Разность Возвращает отношение, содержащее все кортежи, которые принадлежат первому из двух заданных отношений ине принадлежат второму.

Соединение Возвращает отношение, содержащее все возможные кортежи, которые представляют собой комбинацию атрибутов двух кортежей принадлежащих двум заданным отношениям, при условии, что в этих двух комбинируемых кортежах присутствуют одинаковые значения в одном или нескольких общих для исходных отношений атрибутах (причем эти общие значения в результирующем кортеже появляются один раз, а не дважды)

Деление Для заданных двух унарных отношений и одного бинарного возвращает отношение, содержащее все кортежи из первого унарного отношения, которые содержатся также в бинарном отношении и соответствуют всем кортежам во втором унарном отношении.

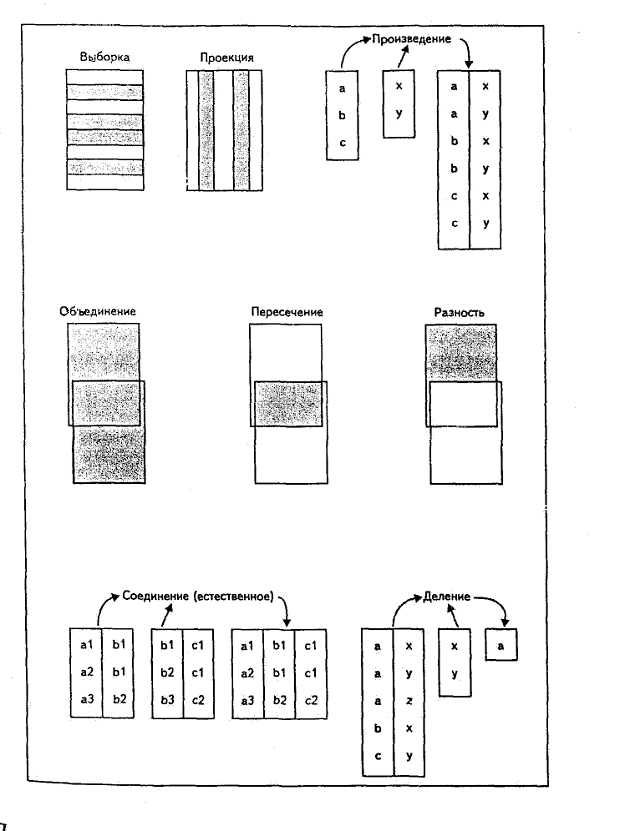
Рис. 5. Первоначальные восемь операторов (обзор).

Дата добавления: 2014-01-11