
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ №2
|
|
|
|
Способ №1
| Десятичное число | Двоичное число | Комментарии |
| 7(10) | 0111(2) | множимое |
| 3(10) | 0011(2) | множитель |
| номера цифр множителя | ||
| 1ое – ЧП | ||
| 2ое – ЧП | ||
| 3ое – ЧП | ||
| 4ое – ЧП | ||
| 21(10) 0010101(2) | сумма ЧП - произведение | |
Рисунок 4.21 - Умножение, начиная с младшей цифры множителя и сдвиг частичных произведений влево
| Десятичное число | Двоичное число | Комментарии |
| 7(10) | 0111(2) | множимое |
| 3(10) | 0011(2) | множитель |
| номера цифр множителя | ||
| 1ое – ЧП | ||
| 2ое – ЧП | ||
| 3ое – ЧП | ||
| 4ое – ЧП | ||
| 21(10) 0010101(2) | сумма ЧП - произведение | |
Рисунок 4.22 - Умножение, начиная со старшей цифры множителя и сдвиг частичных произведений вправо.
В отличие от ручного умножения, операционное устройство компьютера не может просуммировать сразу (s) частичных произведений, как это делает человек. Обычный сумматор, как правило, рассчитан на одновременное сложение только двух операндов. Если нужно получить сумму нескольких слагаемых, то происходит накопление суммы: сначала в сумматор записывается первое слагаемое, к нему прибавляется второе, затем к полученной сумме прибавляется третье слагаемое и так до получения полной суммы.
Длина произведения s-битных сомножителей равна 2s бит:
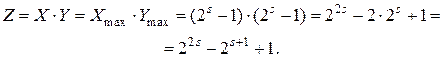 (4.5)
(4.5)
Поскольку умножение на (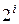 ) эквивалентно сдвигу влево, то вычисление произведения (Z) сводится к формированию частичных произведений (
) эквивалентно сдвигу влево, то вычисление произведения (Z) сводится к формированию частичных произведений ( ), их сдвигу и суммированию с учетом весов, определяемых величинами (
), их сдвигу и суммированию с учетом весов, определяемых величинами (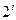 ).
).
 (4.6)
(4.6)
Умножение реализуется циклическим процессом, на каждом шаге которого:
- анализируется очередной бит (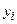 ) множителя;
) множителя;
- в зависимости от его значения происходит (yi=1) или нет (yi=0) прибавление множимого к предыдущей сумме частичных произведений;
- производится изменение взаимного положения множимого (X) и суммы частичных произведений с учетом веса (2i).
Таким образом, умножение в двоичной системе счисления естественным образом сводится к двум операциям - сложению и сдвигу чисел.
В соответствии со способом формирования суммы частичных произведений - (ЧП), возможны четыре варианта умножения. Они различаются тем, с каких разрядов множителя (Y) (младших или старших) начинается умножение, и что сдвигается (множимое или сумма ЧП).
Варианты умножения, начиная с младших или старших разрядов множителя, называются еще умножением младшими и старшими разрядами вперед соответственно.
Схемы выполнения операции умножения двоичных беззнаковых чисел представлены на рис. 4.23.
При умножении младшими разрядами вперед производятся последовательные сдвиги множителя вправо, вследствие чего в младшем разряде регистра множителя последовательно появляются все его цифры, начиная с младшей. Т.о., в специальной схеме анализа значения текущей цифры множителя нужно анализировать только состояние младшего разряда соответствующего регистра.
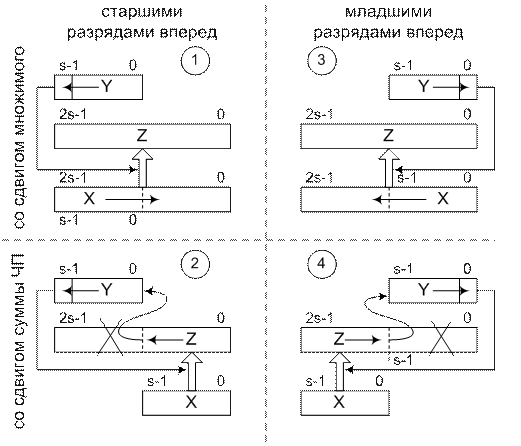
Рисунок 4.23 - Схемы выполнения операции умножения двоичных беззнаковых чисел
Соответственно, при умножении старшими разрядами вперед должен анализироваться старший разряд множителя.
Схема 1
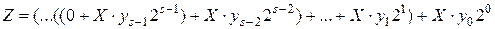 . (4.7)
. (4.7)
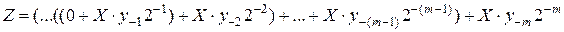 . (4.8)
. (4.8)
Время выполнения операции умножения:
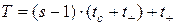 (4.9)
(4.9)
где (tс) - время, затрачиваемое на выполнение операции сдвига на один разряд;
(t+) - время, затрачиваемое на выполнение операции сложения.
Схема 2
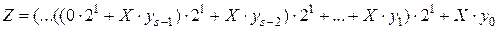 . (4.10)
. (4.10)
 (4.11)
(4.11)
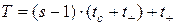 . (4.12)
. (4.12)
Схема 3
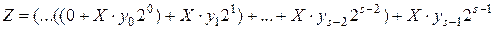 . (4.13)
. (4.13)
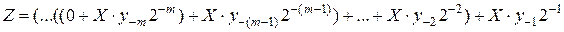 . (4.14)
. (4.14)
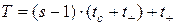 . (4.15)
. (4.15)
Схема 4
 . (4.16)
. (4.16)
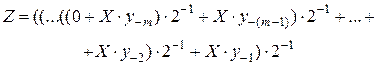 . (4.17)
. (4.17)
 . (4.18)
. (4.18)
Рассмотрим на примере два базовых алгоритма умножения в компьютерных системах двоичных беззнаковых чисел:
Алгоритм №1. Алгоритм умножения младшими разрядами вперед, со сдвигом суммы ЧП вправо.
1. Исходное значение суммы (ЧП) принимается равным (0), счетчику тактов - (Сч.Т) присваивается значение, равное числу разрядов множителя.
2. Анализируется младшая разрядная цифра множителя. Если она равна (1), то к сумме (ЧП) прибавляется множимое, совмещенное по старшим разрядам; если (0) - прибавление не производится.
3. Производится сдвиг множителя и суммы ЧП вправо на (1) разряд. Содержимое (Сч.Т) уменьшается на (1).
4. Анализируется содержимое (Сч.Т). Если оно не равно (0), то переход к (п.2), иначе - (п.5).
5. Умножение закончено, младшая часть произведения находится на месте множителя, а старшая - на месте суммы (ЧП). Например: необходимо перемножить два беззнаковых числа (7∙3=21). Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: Х = 7 - множимое, Y = 3 - множитель, Z = 21 - произведение. Если (X) и (Y) равняется четырем битам, то как было отмечено выше (Z) должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя. Алгоритм умножения приведен в табл. 4.1.
Таблица 4.1 - Алгоритм умножения со сдвигом вправо двоичных беззнаковых чисел
| Регистр (В) множимое X | Регистр (С) множитель Y | Регистр (А) произведение Z | Счетчик тактов (Сч.Т) | Комментарии | ||||||
| множимое | ||||||||||
| 1Я СЧП | ||||||||||
| 1ЫЙсдвиг СЧП | ||||||||||
| множимое | ||||||||||
| 2Я СЧП | ||||||||||
| 2 ОЙсдвиг СЧП | ||||||||||
| 3 ИЙсдвиг СЧП | ||||||||||
| 4ЫЙсдвиг СЧП | ||||||||||
| СТОП | ||||||||||
Алгоритм №2. Алгоритм умножения старшими разрядами вперед, со сдвигом суммы ЧП влево.
1. Исходное значение суммы (ЧП) принимается равным (0), (Сч.Т) присваивается значение, равное числу разрядов множителя.
2. Производится сдвиг суммы (ЧП) влево на (1) разряд.
3.Анализируется старшая разрядная цифра множителя. Если она равна (1), то к сумме (ЧП) прибавляется множимое, совмещенное по младшим разрядам; если (0) - прибавление не производится.
4.Производится сдвиг множителя влево на (1) разряд. Содержимое (Сч.Т) уменьшается на (1).
5.Анализируется содержимое (Сч.Т). Если оно не равно (0), то переход к (п.2), иначе - (п.6).
6.Умножение закончено, произведения находится на месте суммы (ЧП), которая имеет удвоенную разрядность. Например: необходимо перемножить два беззнаковых числа (7∙3=21). Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: Х = 7 - множимое, Y = 3 - множитель, Z = 21 - произведение. Если (X) и (Y) равняется четырем битам, то как было отмечено выше (Z) должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя. Алгоритм умножения приведен в табл. 4.1.
Таблица 4.2 - Алгоритм умножения со сдвигом влево двоичных беззнаковых чисел
| Регистр (В) множимое X | Регистр (С) множитель Y | Регистр (А) произведение Z | Счетчик тактов (Сч.Т) | Комментарии | ||||||
| 1ЫЙсдвиг СЧП | ||||||||||
| 2 ОЙсдвиг СЧП | ||||||||||
| 3 ИЙсдвиг СЧП | ||||||||||
| 4ЫЙсдвиг СЧП | ||||||||||
| 5ЫЙсдвиг СЧП | ||||||||||
| множимое | ||||||||||
| 1Я СЧП | ||||||||||
| 6ОЙ сдвиг СЧП | ||||||||||
| множимое | ||||||||||
| 2Я СЧП | ||||||||||
| СТОП | ||||||||||
Для закрепления материала рекомендуется выполнить следующие упражнения:
| 1. Перевести в двоичную систему счисления и вычислить выражение: ((15(10) – 10(10)) * (18(10) – 11(10))). |
| 2. Перевести в двоичную систему счисления и вычислить выражение: ((21(10) – 15(10)) * (18(10) – 11(10))). |
| 3. Перевести в двоичную систему счисления и вычислить выражение: ((19(10) – 15(10)) * (18(10) – 11(10))). |
| 4. Перевести в двоичную систему счисления и вычислить выражение: ((18(10) – 11(10)) * (18(10) – 14(10))). |
| 5. Перевести в двоичную систему счисления и вычислить выражение: ((23(10) – 17(10)) * (21(10) – 15(10))). |
| 6. Перевести в двоичную систему счисления и вычислить выражение: ((14(10) – 11(10)) * (18(10) – 10(10))). |
4.5 Деление двоичных беззнаковых чисел в компьютерных системах
Деление мантисс чисел в форме с фиксированной запятой выполняется над абсолютными величинами операндов, представленными, чаще всего, прямым кодом.
Подобно умножению, деление в компьютерных системах реализуется как многошаговый процесс выполнения операций суммирования, сдвига и других элементарных операций.
В отличие от умножения этот процесс имеет итеративный характер, так как результат деления в большинстве случаев не может быть точно представлен числом конечной длины.
Как правило, формальным признаком окончания операции деления принимается количество сдвигов: при достижении числа сдвигов, равного количеству разрядов в частном, операция деления завершается.
Обозначим X - делимое, Y - делитель, а Z - частное. Тогда:
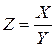 . (4.19)
. (4.19)
Пусть (X), (Y) и (Z) являются беззнаковыми числами.
Операция деления характеризуется также дополнительным результатом (R) - остатком.
В практической реализации выделяют два типа операции деления:
- первый тип это когда делимое, делитель и частное имеют одну и ту же длину (s);
- второй тип это когда делимое имеет длину (2s) - удвоенную по сравнению с делителем и частным. Рассмотрим случай 1.
 ,
,  . (4.20)
. (4.20)
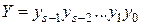 ,
,  . (4.21)
. (4.21)
 ,
,  . (4.22)
. (4.22)
 ,
,  . (4.23)
. (4.23)
 . (4.24)
. (4.24)
Для того, чтобы деление было корректным, т.е. чтобы частное не превысило разрядную сетку, необходимо обеспечить выполнение условия:
 . (4.25)
. (4.25)
или
 . (4.26)
. (4.26)
В противном случае будет иметь место переполнение разрядной сетки.
Переполнение исключено, если делимое и делитель имеют одинаковую длину. Как особый случай переполнения рассматривают попытку деления на нуль.
По существу, деление сводится к последовательности вычитаний делителя вначале из делимого, а затем из остатков.
Цифра ( ) частного определяется следующим образом: если текущий остаток (
) частного определяется следующим образом: если текущий остаток ( ) больше или равен делителю, цифра частного равна (1), если меньше, то цифра частного равна (0).
) больше или равен делителю, цифра частного равна (1), если меньше, то цифра частного равна (0).
При этом операция сравнения реализуется посредством операции вычитания.
Так как частное можно определить только со старших разрядов, существует два варианта деления представленных на рис. 4.9:
- с неподвижным делимым (частичным остатком) и сдвигаемым вправо делителем;
- с неподвижным делителем и сдвигаемым влево делимым (частичным остатком).
В зависимости от способа обработки отрицательного частичного остатка, различают два алгоритма деления:
- алгоритм №1, с восстановлением остатка;
- алгоритм №2 без восстановления остатка.
Деление с восстановлением остатка заключается в следующем, если на очередном шаге получен положительный остаток, то в очередную цифру частного записывается (1), а остаток становится «предыдущим» для следующего шага.
Данный шаг на этом заканчивается.
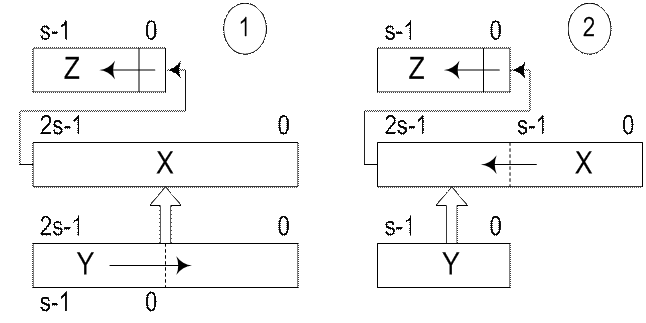
Рисунок 4.9 - Схемы деления двоичных беззнаковых чисел
Если текущий остаток отрицателен, то в очередную цифру частного записывается (0), а к остатку прибавляется делитель для восстановления предыдущего, сдвинутого влево остатка, который становится «предыдущим» для следующего шага.
Таким образом, отрицательный остаток аннулируется, поскольку он выполнил свою функцию сигнализатора о соотношении модулей остатка и делителя и больше не нужен.
Алгоритм №1. Деление целых двоичных беззнаковых чисел методом с восстановлением остатка.
1. Исходное значение частного (Z) полагается равным (0). (Сч.Т) присваивается значение (s). Исходное значение частичного остатка (R0) полагается равным (s) старшим разрядам делимого.
2. Выполняется пробное вычитание делителя (Y) из исходного значения частичного остатка – (ЧО). Положительная разность указывает на то, что частное превысит (s-разрядную сетку), и будет выполнено прерывание. Если же результат вычитания отрицательный, то деление можно выполнять.
3. Восстанавливается исходное значение (ЧО) прибавлением делителя к полученному отрицательному остатку.
4. (ЧО) удваивается путем сдвига на один разряд влево.
5. Из (ЧО) вычитается делитель и анализируется знак результата вычитания: если остаток положительный, то очередная цифра частного равна (1), иначе – (0).
6. Частное сдвигается влево с занесением очередной полученной цифры частного в освободившийся младший разряд. (Сч.Т) уменьшается на (1).
7. Если полученный остаток отрицателен, то восстанавливается предыдущий положительный остаток прибавлением делителя к отрицательному остатку.
8. (Пп. 4-7) последовательно выполняются до получения всех цифр частного, пока (Сч.Т) не станет равным (0).
9. Если последний остаток от деления отрицателен, то восстанавливается предыдущий положительный остаток, который будет окончательным остатком от деления.
Недостатки:
- нерегулярность выполнения операций, что усложняет устройство управления (для получения одной цифры частного необходимо выполнять либо одно вычитание и сдвиг, либо одно вычитание, одно сложение и сдвиг);
- относительно малая скорость деления, т.к. в среднем половина шагов будет содержать операцию восстановления остатка.
T=(s+l)(l,5t++tc)–tc.
Например: необходимо разделить два беззнаковых числа (21:7=3).
Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
Х = 21 – делимое;
Y = 7 – делитель;
Z = 3 – частное.
Если (Z) и (Y) равняется четырем битам, то как было отмечено выше (X) должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Алгоритм деления приведен в табл. 4.3.
Таблица 4.3 - Алгоритм деление целых двоичных беззнаковых чисел методом с восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| <0 | ||||||||||||||||||||
| <0 | ||||||||||||||||||||
| <0 | ||||||||||||||||||||
| >0 | ||||||||||||||||||||
| >0 | ||||||||||||||||||||
| СТОП | ||||||||||||||||||||
Деления без восстановления остатка заключается в следующем, исходной предпосылкой для использования данного метода является желание избавиться от процедуры восстановления остатка.
Благодаря этому, длительность деления можно существенно уменьшить по сравнению с вышеприведенной оценкой (за счет исключения "лишней" операции восстановления остатка), используя алгоритм деления без восстановления остатка.
Проанализируем шаг деления, при котором текущий остаток оказался отрицательным. Обозначим:
- ( ) - предыдущий остаток;
) - предыдущий остаток;
- ( ) - текущий;
) - текущий;
- ( ) - последующий.
) - последующий.
Пусть:
 . (4.27)
. (4.27)
При этом, в соответствии с правилом деления, должны выполняться три действия:
- восстановление предыдущего (сдвинутого влево) остатка:
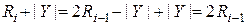 . (4.28)
. (4.28)
- сдвиг восстановленного остатка влево на один разряд:
 . (4.29)
. (4.29)
- вычитание модуля делителя из полученной кодовой комбинации:
 . (4.30)
. (4.30)
Таким образом, требуется перейти от текущего остатка:
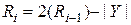 . (4.31)
. (4.31)
к последующему виду (4.31), избавившись от операции восстановления.
Если первым действием является сдвиг отрицательного остатка (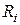 ) влево, то:
) влево, то:
 . (4.32)
. (4.32)
Правая часть (4.32) отличается от требуемого вида величиной |Y|.
Поэтому вторым действием будет корректировка (4.33):
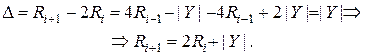 . (4.33)
. (4.33)
Сформулируем общее правило.
Чтобы определить цифру частного в некотором разряде, необходимо сдвинуть логически ( ) влево на один разряд, а затем прибавить к нему код делителя, которому приписывается знак, противоположный знаку предыдущего остатка; если полученный (
) влево на один разряд, а затем прибавить к нему код делителя, которому приписывается знак, противоположный знаку предыдущего остатка; если полученный (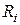 ) положительный, то в частном проставляется (1), если же отрицательный, - то (0).
) положительный, то в частном проставляется (1), если же отрицательный, - то (0).
Алгоритм №2. Деления целых двоичных чисел методом без восстановления остатка
1-2. Аналогично п.п. 1, 2 предыдущего.
3. Аналогично п. 4.
4. Из частичного остатка вычитается делитель, если остаток положительный, или к частичному остатку прибавляется делитель, если остаток отрицательный.
5. Частное сдвигается; в младший разряд заносится очередная цифра частного (1 — при положительном остатке, 0 — при отрицательном);
6. П.п. 3-5 последовательно выполняются для получения всех цифр частного, пока (Сч.Т) не станет равен (0).
7. Аналогично последнему пункту предыдущего алгоритма.
Реализация данного алгоритма не требует никаких дополнительных аппаратурных затрат.  .
.
Например: необходимо разделить два беззнаковых числа (21:7=3).
Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
Х = 21 – делимое;
Y = 7 – делитель;
Z = 3 – частное.
Если (Z) и (Y) равняется четырем битам, то как было отмечено выше (X) должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Алгоритм деления приведен в табл. 4.4.
Таблица 4.4 - Алгоритм деление целых двоичных беззнаковых чисел методом без восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| <0 | ||||||||||||||||||||
| <0 | ||||||||||||||||||||
| <0 | ||||||||||||||||||||
| >0 | ||||||||||||||||||||
| >0 | ||||||||||||||||||||
| СТОП | ||||||||||||||||||||
Для закрепления материала рекомендуется выполнить следующие упражнения:
| 1. Перевести в двоичную систему счисления и вычислить выражение: ((15(10) – 10(10)) * (18(10) – 11(10)))/5(10). |
| 2. Перевести в двоичную систему счисления и вычислить выражение: ((21(10) – 15(10)) * (18(10) – 11(10)))/6(10). |
| 3. Перевести в двоичную систему счисления и вычислить выражение: ((19(10) – 15(10)) * (18(10) – 11(10)))/7(10). |
| 4. Перевести в двоичную систему счисления и вычислить выражение: ((18(10) – 11(10)) * (18(10) – 14(10)))/4(10). |
| 5. Перевести в двоичную систему счисления и вычислить выражение: ((23(10) – 17(10)) * (21(10) – 15(10)))/6(10). |
| 6. Перевести в двоичную систему счисления и вычислить выражение: ((14(10) – 11(10)) * (18(10) – 10(10)))/3(10). |
4.6 Умножение двоичных знаковых чисел в компьютерных системах
При выполнении операции умножения знаковых чисел исходные сомножители могут быть представлены в ПК, ОК или ДК:
 . (4.34)
. (4.34)
При данном способе умножения знаковые и числовые разряды обрабатываются отдельно. Для определения знака произведения осуществляют суммирование (по модулю 2) цифр, записанных в знаковых разрядах операндов. Модуль произведения получают, перемножая модули сомножителей в соответствии с одним из рассмотренных ранее алгоритмов:
 . (4.35)
. (4.35)
Определение знака произведения показано в табл. 4.5. Где (0) - обозначает (+), а (1) – обозначает (-).
Таблица 4.5 – Определение знака произведения
0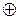 0=0 0=0
|
0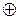 1=1 1=1
|
1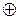 0=1 0=1
|
1 1=0 1=0
|
Однако в современных компьютерах операнды в памяти обычно хранятся в ДК, что продиктовано, в частности, удобством выполнения операции сложения (учитывая автоматическое формирование знака суммы). Для того, чтобы умножить два числа, представленных в ДК можно использовать следующий прием: перед выполнением операции умножения исходные числа преобразуют в ПК, затем их перемножают, а результат далее переводят в ДК.
Такой прием не является эффективным. Поэтому на практике чаще всего используют специальные алгоритмы умножения чисел в дополнительных кодах. Алгоритмы корректного умножения операндов в ДК можно разделить на две группы:
- алгоритмы первой группы это алгоритмы с обработкой знаковых разрядов отдельно от числовых;
- алгоритмы второй группы это алгоритмы с обработкой знаковых разрядов вместе с числовыми. Т.е., на сумматоре дополнительных кодов в процессе перемножения машинных изображений операндов получают одновременно знаковую и числовую части произведения.
Теорема: произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительных сомножителей. Если хотя бы один сомножитель отрицателен, то произведение чисел на сумматоре дополнительных кодов получается прибавлением поправки (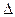 ) к произведению дополнительных кодов сомножителей. Рассмотрим арифметическое обоснование алгоритмов первой группы при различных вариантах комбинаций знаков операндов. С этой целью у операндов отбрасывается знаковая цифра и выполняется умножение полученных псевдомодулей по одному из известных алгоритмов. Результат такого умножения назовем псевдопроизведением (
) к произведению дополнительных кодов сомножителей. Рассмотрим арифметическое обоснование алгоритмов первой группы при различных вариантах комбинаций знаков операндов. С этой целью у операндов отбрасывается знаковая цифра и выполняется умножение полученных псевдомодулей по одному из известных алгоритмов. Результат такого умножения назовем псевдопроизведением (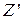 ). Обозначим вес знакового разряда сомножителей (
). Обозначим вес знакового разряда сомножителей ( ). Тогда, в соответствии с рассмотренным ранее правилом формирования дополнительного кода, отрицательные сомножители будут представлены в ДК следующим образом:
). Тогда, в соответствии с рассмотренным ранее правилом формирования дополнительного кода, отрицательные сомножители будут представлены в ДК следующим образом:
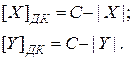 . (4.36)
. (4.36)
При удалении знакового разряда получаем псевдомодули:
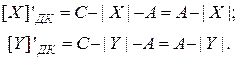 . (4.37)
. (4.37)
Всего возможны четыре варианта сочетания знаков сомножителей:
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2390; Нарушение авторских прав?; Мы поможем в написании вашей работы!