Машины Тьюринга

Одноленточная детерминированная машина Тьюринга (ДМТ) представляет собой абстрактное логическое устройство, которое состоит из:

1) неограниченной в обе стороны ленты, разделенной на одинаковые пронумерованные ячейки;

2) читающей / пишущей головки;

3) управляющего устройства с конечным числом состояний.

Схематически ДМТ можно представить в виде рисунка

Программу для ДМТ определяют следующие компоненты:

1) G – конечное множество символов, записываемых на ленте, 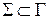– множество входных символов, – выделенный пустой символ;

2) Q – конечное множество состояний, в котором выделено начальное состояние 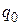и два конечных – ;

3) функция переходов .

Т.е. .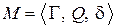

Порядок работы ДМТ под управлением программы .

1. Входное слово 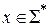записывается на ленте в ячейках с номерами 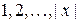, все другие ячейки содержат пустой символ. Управляющее устройство находится в состоянии , а читающая/пишущая головка – над ячейкой с номером 1.

2. Если текущее состояние q не совпадает с одним из конечных состояний, то машина переходит в следующее состояние, определяемое согласно функции переходов. Пусть 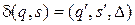, где s – считанный головкой символ из текущей ячейки. Тогда управляющее устройство переходит в состояние 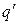, головка вместо символа s записывает символ 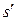и сдвигается на одну ячейку влево, если 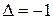, или вправо, если 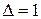. Затем, текущим становится состояние .

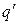3. Если 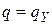, то вычисления заканчиваются с результатом “да”, если , то – с результатом “нет”.

В качестве примера рассмотрим упоминавшуюся выше задачу “делимости на 4”. Построим ДМТ-программу для решения этой задачи.

Для представления чисел будем использовать символы 0 и 1, а в качестве схемы кодирования – двоичную запись числа. Значит, , .

Опишем словесно действия ДМТ, а затем формализуем в виде программы . Число делится нацело на 4, если два последних символа в его двоичном представлении являются нулями. Поэтому, вначале машина будет считывать, повторять все символы входного слова и двигаться вправо, пока не дойдёт до пустого символа. После чего будет выполняться движение влево и анализ последнего и предпоследнего символа с последующей заменой его на символ b. Если хотя бы один из этих символов не равен 0, то результирующее состояние – , в противном случае – 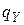. При любом конечном состоянии результатом на ленте будет частное от целочисленного деления, причём, если , то им является пустое слово, т.е. 0.

Представим функцию переходов наглядно в виде ориентированного графа. Вершинами графа будут являться состояния управляющего устройства, дуги графа означают переход из одного состояния в другое, причём, над каждой дугой будем писать символ(ы), по которому выполняется переход, а после знака ® – замещающий символ и направление движения головки.

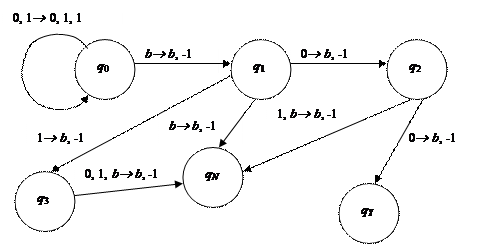Следовательно, 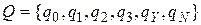. Функцию переходов d можно также задать табличным способом.

			b
q 0	(q 0, 0, 1)	(q 0, 0, 1)	(q 1, 0, 1)
q 1	(q 2, 0, 1)	(q 3, 0, 1)	(qN, 0, 1)
q 2	(qY, 0, 1)	(qN, 0, 1)	(qN, 0, 1)
q 3	(qN, 0, 1)	(qN, 0, 1)	(qN, 0, 1)

Программа , имеющая входной алфавит S, принимает слово 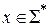в том и только том случае, когда, будучи применённой ко входу x, она останавливается в состоянии 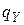. Язык 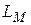, распознаваемый программой , определяется следующим образом

.

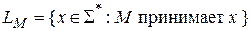Если , то работа программы может либо завершиться в состоянии , либо бесконечно продолжаться без остановки. Будем говорить, что ДМТ-программа решает задачу распознавания P при схеме кодирования e, если останавливается для любых 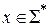и .

Дата добавления: 2014-01-11