Шершнев В. Г

Напечатано в ГОУ ВПО «РЭА им. Г. В. Плеханова»

Ш Математический анализ. Часть 2. Интегральное исчисление.

Курс лекций для дистанционной формы обучения. – М.: ГОУ ВПО

Данное пособие составлено на основе лекций, читаемых автором на экономических факультетах РЭА им. Г. В. Плеханова. Содержит теоретический материал по разделам математического анализа: неопределенный и определенный интегралы, дифференциальные уравнения и ряды. Приводится решение характерных заданий. Пособие соответствует программе по математическому анализу для студентов экономических специальностей.

Календарно-тематический план.................................
Глава 4. Неопределенный интеграл.............................
4.1.Определение неопределенного интеграла.......................
4.2. Свойства неопределенного интеграла.Таблица интегралов........
4.3. Методы интегрирования.....................................
4.3.1. Метод непосредственного интегрирования..................
4.3.2. Метод замены переменной................................
4.3.3. Интегрирование функций, содержащих квадратный трехчлен...
4.3.4. Метод интегрирования по частям неопределенных интегралов..
4.3.5. Интегрирование дробно-рациональных функций..............
4.3.6. Об интегрировании простых дробей........................
4.3.7. Интегрирование иррациональных функций..................
4.3.8. Интегрирование тригонометрических функций................
4.3.9. Интегрирование иррациональных функций с помощью тригонометрических подстановок........................................
4.4. Об интегрировании в конечном виде...........................
Глава 5. Определенный интеграл...............................
5.1. Задачи, приводящие к понятию определенного интеграла.........
5.2. Интегральные суммы, их свойства............................
5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона – Лейбница.......................................
5.4. Свойства определенного интеграла............................
5.5. Методы интегрирования определенных интегралов.............
5.6. Несобственные интегралы с бесконечными пределами интегрирования.........................................................
5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования......................................
5.8. Несобственные интегралы от разрывных функций, неограниченных в точках разрыва...............................................
5.9. Теоремы о сходимости несобственных интегралов от разрывных функций......................................................
5.10. Геометрические приложения определенных интегралов.........
5.10.1. Вычисление площадей фигур..............................
5.10.2. Вычисление объемов тел вращения.........................
5.10.3. Длина дуги кривой......................................
5.11. Численные методы нахождения определенных интегралов......
5.11.1. Формулы прямоугольников...............................
5.11.2. Формула трапеций......................................
5.11.3. Формула Симпсона......................................
5.12. Производная интеграла, зависящего от параметра...............
Глава 6. Двойные интегралы...................................
6.1. Определение двойного интеграла.............................
6.2. Геометрический смысл двойного интеграла.....................
6.3. Свойства двойных интегралов................................
6.4. Вычисление двойных интегралов.............................
6.5. Двойные несобственные интегралы с бесконечными пределами интегрирования..................................................
Глава 7. Дифференциальные уравнения.........................
7.1. Общие понятия............................................
7.2. Дифференциальные уравнения первого порядка.................
7.3. Задача Коши. Теорема о существовании и единственности решения дифференциального уравнения первого порядка.....................
7.4. Дифференциальные уравнения с разделяющимися переменными..
7.5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)............................
7.6. Линейные дифференциальные уравнения первого порядка........
7.7. Уравнение Бернулли........................................
7.8. Дифференциальные уравнения первого порядка в полных дифференциалах.....................................................
7.9. Дифференциальные уравнения высших порядков................
7. 10. Дифференциальное уравнение вида ...............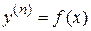
7.11. Дифференциальные уравнения второго порядка, приводимые к дифференциальным уравнениям первого порядка....................
7.12. Линейные дифференциальные уравнения n -ого порядка. Свойства их решений................................................
7.13. Линейная зависимость функций. Определитель Вронского.......
7.14. Структура общего решения линейного неоднородного дифференциального уравнения n -ого порядка...............................
7.15. Комплексные числа и действия над ними......................
7.16. Показательная функция с комплексным показателем............
7.17. Показательная форма комплексного числа. Формула Эйлера.....
7.18. Общее решение линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами.............
7.19. Частное решение линейного неоднородного дифференциального уравнения n -го порядка с постоянными коэффициентами.............
7.20. Метод Эйлера численного интегрирования дифференциальных уравнений.....................................................
Глава 8. Числовые ряды.......................................
8.1. Основные понятия..........................................
8.1. 1. Определение числового ряда..............................
8.1.2. Сходимость числового ряда. Сумма ряда....................
8.1.3. Свойства сходящихся рядов...............................
8.2. Необходимый признак сходимости числового ряда..............
8.3. Классификация числовых рядов в зависимости от знаков их членов
8.4. Достаточные признаки сходимости знакоположительных числовых рядов.........................................................
8.4.1. Признаки сравнения рядов................................
8.4.2. Признак Даламбера сходимости знакоположительных рядов....
8.4.3. Радикальный признак Коши сходимости числового ряда.......
8.4.4. Интегральный признак Коши..............................
8.5. Знакочередующиеся ряды. Теорема Лейбница..................
8.6. Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда...................................................
Глава 9. Степенные ряды.......................................
9.1. Функциональные ряды. Общие понятия........................
9.2. Равномерная сходимость функциональных рядов. Теорема Вейерштрасса.......................................................
9.3. Теорема Абеля о виде области сходимости степенного ряда.......
9.4. Радиус и область сходимости степенного ряда..................
9.5. Ряды Тейлора и Маклорена..................................
9.6. Разложение в ряд Маклорена основных элементарных функций...
9.7. Применение рядов для приближенных вычислений..............
Вопросы к экзамену.............................................
Литература....................................................