Задачи, приводящие к понятию определенного интеграла

Рассмотрим две задачи, одна с геометрическим смыслом, другая с механическим смыслом.

1. Задача о площади криволинейной трапеции.

Пусть функция 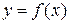является непрерывной на отрезке 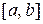. Требуется найти площадь криволинейной трапеции, ограниченной линиями: 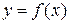, 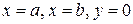(рис. 57).

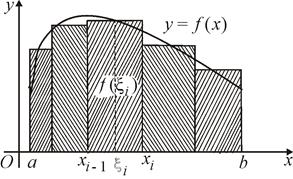
Рис. 57

При нахождении площади этой трапеции выполним следующие действия:

1. Разобьем отрезок [ a, b ] с помощью произвольно выбранных точек

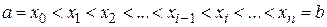на n элементарных отрезков длиной

.

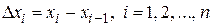2. На каждом элементарном отрезке выберем произвольно точку 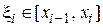, вычислим значение функции в этой точке 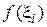и найдем приближенно площадь элементарной криволинейной трапеции как площадь прямоугольника .

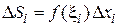3. Найдем приближенно площадь всей криволинейной трапеции

.

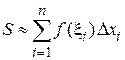4. Перейдем к пределу при 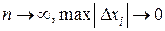, найдем точное значение площади криволинейной трапеции

.

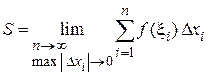2. Задача о пройденном пути.

Пусть известна зависимость скорости движения от времени 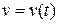на отрезке времени .Требуется найти длину пути, пройденного за время 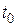от до Т.

1. Разобьем отрезок времени с помощью произвольно выбранных моментов времени

на n элементарных интервалов времени продолжительностью

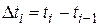, i = 1, 2, …, n.

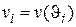2. На каждом элементарном интервале времени выберем произвольно момент времени , вычислим скорость и найдем приближенно путь пройденный за элементарный интервал времени

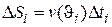, i = 1, 2, …, n.

3. Найдем приближенно путь, пройденный за отрезок времени ,

.

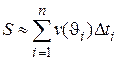4. Перейдем к пределу при 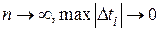, найдем точное значение пройденного пути

.

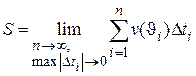Как можно заметить, в рассмотренных задачах с геометрическим и механическим смыслом, решение выполняется в аналогичном порядке. Поэтому можно выполнить подобные действия независимо от прикладного смысла задачи. Обобщим полученные результаты.

Дата добавления: 2014-01-11