Графические методы расчета цепей с нелинейными резистивными двухполюсниками

Графические методы статического анализа

СТАТИЧЕСКИЙ АНАЛИЗ ЭЛЕКТРОННЫХ СХЕМ

Под статическим режимом схемы понимают режим, при котором входные сигналы имеют нулевые значения и существуют лишь воздействия от источников питания. Расчет статического режима схемы имеет важное значение при ее исследовании. Результатами статического анализа схемы являются значения постоянных составляющих токов и напряжений схемы. Статический режим схемы определяет начальные условия при ее анализе в области малого и большого сигналов.

Для анализа статического режима нелинейных электронных схем применяют графические и аналитические методы. При использовании графических методов, отличающихся наглядностью и точностью, затруднена оценка влияния параметров компонентов схемы на статический режим. Использование аналитических методов, основанных на аппроксимации нелинейной зависимости и формировании математической модели схемы, позволяют исследовать влияние различных параметров на режим схемы по постоянному току.

Задача нахождения начальных постоянных напряжений и токов на внешних зажимах нелинейных полупроводниковых или электронных приборов, входящих в электрическую цепь, сводится к задаче анализа режима постоянного тока в исследуемой цепи, т. е., к анализу нелинейной резистивной цепи с источниками постоянного напряжения или (и) тока. Решаются подобные задачи обычно с использованием графических построений.

Ниже рассматривается задача анализа режима постоянного тока в электрической цепи с одним нелинейным двухполюсником - нелинейным резистивным элементом (НЭ). Его ВАХ считается известной и заданной графически.

Рис. 3.1

Рассмотрим простейшую электрическую цепь, изображенную на рис. 3.1. В нее входят источник постоянного напряжения с задающим напряжением U _г, линейный резистивный элементр R и нелинейный резистивный элемент, в котором подлежат определению постоянные напряжение U = U₀ и ток I = I₀.

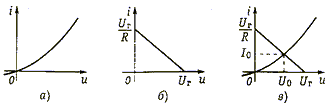
Рис. 3.2

Пусть однозначная ВАХ нелинейного резистивного элемента имеет вид, показанный на рис. 3.2, а.

Согласно схеме (рис. 3.1) напряжение U = U_г - RI, и ток в элементе R связан с напряжением U на зажимах НЭ зависимостью I = (U_г - U/R), представляющей собой прямую, проходящую через точки U _г на оси абсцисс и U _г/ R - на оси ординат. Поскольку нелинейный и линейный элементы соединены последовательно, то ВАХ НЭ и прямая I = (U_г -U/R), определяющие один и тот же ток, удовлетворяются одновременно, чему на графиках рис. 3.2, в соответствует точка их пересечения. Она и определяет искомые значения постоянных напряжения U ₀ и тока I ₀ в нелинейном резисторе, или, как принято говорить, его рабочую точку.

Графические построения, связанные с решением задачи, всегда выполнимы, а найденное ее решение - единственное.

Рабочая точка нелинейного резистора изменяется как с изменением сопротивления R, так и с изменением задающего напряжения источника U _г. Изменение сопротивления R приводит к изменению наклона зависимости I = (U_г - U/R) и смещению рабочей точки на вольт-амперной характеристике нелинейного резистора (см. рис. 3.3, а). Изменение задающего напряжения на величину D U _г вызывает перемещение той же зависимости параллельно самой себе и изменение тока и напряжения в нелинейном резисторе соответственно на величины D U и D I (см. рис. 3.3, б).

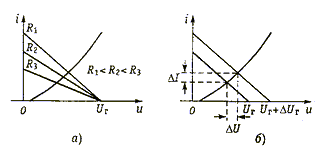
Рис. 3.3

Напомним, что отношение бесконечно малого приращения тока к бесконечно малому приращению напряжения на нелинейном элементе, обусловленных смещением рабочей точки, называется дифференциальной проводимостью (крутизной), а обратное отношение - дифференциальным сопротивлением нелинейного резистора в его рабочей точке.

Отношение постоянных тока и напряжения в рабочей точке нелинейного резистора определяет его статистическую проводимость, а обратное отношение - статическое сопротивление резистора в его рабочей точке.

Статическая проводимость пассивного нелинейного резистора всегда положительна. Положительна и дифференциальная проводимость нелинейного резистора с однозначной вольт-амперной характеристикой в силу возрастающего характера последней. Заметим также, что статическая и дифференциальная проводимости линейного резистора не отличаются одна от другой.

Метод эквивалентного генератора. Изложенная методика определения рабочей точки в цепи с одним линейным и одним нелинейным резистивными элементами распространяется на резистивные цепи с одним резистивным НЭ и произвольным числом линейных резистивных элементов и источников постоянного напряжения или (и) тока, если воспользоваться теоремой об эквивалентном генераторе. Для этого следует внешнюю по отношению к нелинейному двухполюснику линейную активную цепь (см. рис. 3.4, а) заменить эквивалентным генератором с задающим напряжением U _эг и внутренним линейным резистивным эквивалентным сопротивлением R ₃ (рис. 3.4, б). Тогда схема анализируемой цепи не будет отличаться от схемы рис. 3.1, и задача нахождения рабочей точки сводится к рассмотренной выше.

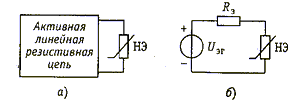
Рис. 3.4

Напряжения и токи в элементах цепи, внешней по отношению к НЭ, можно найти, воспользовавшись теоремой замещения. Для этого нелинейный резистивиый элемент следует заменить источником напряжения (источником тока), напряжение (ток) которого равно (равен) найденному значению напряжения (тока) в рабочей точке. Напряжения и токи в линейной части электрической цепи находят любым методом анализа режима постоянного тока.

Метод с использованием эквивалентного генератора, является графоаналитическим, поскольку в нем аналитические методы определения параметров эквивалентного генератора и расчета линейной цепи после замены НЭ источником напряжения или тока сочетаются с графическим методом нахождения рабочей точки.

Пример. Применим метод эквивалентного генератора к схеме рис. 3.5, а, где U₀₁ ⁼ 14 В, J₀₂ = 10 мА. R₁ = 1 кОм, I_H = 10^{- 5} U_H². Из рисунка следует, что напряжение U _эг - при отключении НЭ равно U _эг = J ₀₂ R ₁ + U ₀₁= 24 В, а эквивалентное сопротивление R _Э = R ₁ = 1 кОм. В соответствии со схемой (рис. 3.5, б) имеем I _H = (U _г - U _H)/ R = -10^-3 U _H + 24^. 10^-3.

Рис. 3.5

Построение графиков прямой линии и ВАХ нелинейного элемента показано на рис. 3.5, в. Пересечение этих кривых дает координаты рабочей точки: I _H = 4 мА и U _H = 20 В.

Дата добавления: 2014-01-11