Критерий устойчивости Михайлова

Для анализа устойчивости рассматривается знаменатель схемной функции B (j ω), который получается из полинома (19) заменой p на j ω:

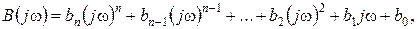(6.2)

где можно выделить вещественную и мнимую часть, а также амплитуду и фазу:

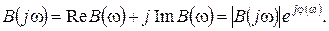
Для конкретного численного значения ω = ω _i имеем комплексное число B (j ω _i), которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой (Re B (ω _i); j Im B (ω _i)). При изменении ω от 0 до ∞ конец вектора B (j ω) выписывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова. При этом годограф начинается, как следует из выражения (6.2), в точке с координатами (b ₀; j 0).

Критерий устойчивости Михайлова формулируется следующим образом: для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении ω от 0 до ∞ начинался на положительном конце вещественной оси в точке b ₀ и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к ∞ в n -ом квадранте.

В устойчивой системе каждый из n корней даст приращение фазы φ _i = + π/2, а общий угол поворота B (j ω) равен + (π/2) n. Вид годографа Михайлова для устойчивой и неустойчивых схем третьего порядка (т.е. у которых знаменатель схемной функции B (p) является полином 3-ей степени) приведен на рис. 6.1.

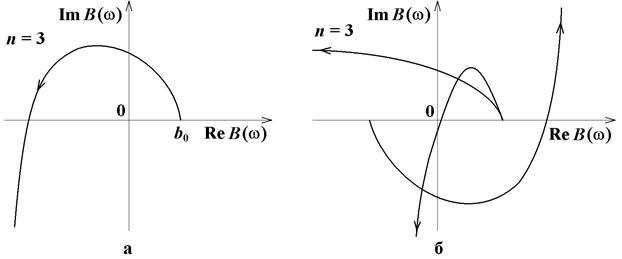
Рис. 6.1. Примеры годографа Михайлова для устойчивой (а) и неустойчивых (б) систем третьего порядка (n = 3)

Оценим устойчивость схемы на рис. 5.1 по критерию Михайлова. Полином знаменателя схемной функции имеет вид

B (p) = pCg ₃ + g ₂ g ₃.

Заменив p на j ω, получим выражение для годографа Михайлова

B (j ω) = j ω Cg ₃ + g ₂ g ₃,

в котором Re B (ω) = g ₂ g ₃ = 1·10^-7 См²; Im B (ω) = ω Cg ₃ = 1·10^-10 Ф·См.

Для построения годографа Михайлова вычислим значения вещественной и мнимой частей при конкретных значениях частоты и занесем их в таблицу.

Таблица. Координаты точек для построения годографа Михайлова

ω					∞
Re B (ω)	1·10^-7	1·10^-7	1·10^-7	1·10^-7	1·10^-7
Im B (ω)		1·10^-10	1·10^-9	1·10^-8	∞

Вид годографа Михайлова для схемы на рис. 5.1 представлен на рис. 6.2.

Рис. 6.2. Годограф Михайлова для схемы на рис. 5.1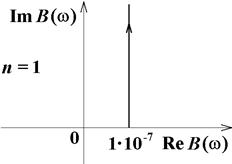

Поскольку годограф начинается на положительном конце реальной оси, попадает в первый квадрант и стремится к ∞ в первом квадранте (у нас n = 1), схема является устойчивой. Данный вывод совпадает с результатами анализа схемы по критерию устойчивости Гурвица.

Дата добавления: 2014-01-11