Полный образ и полный прообраз

Рассмотрим в соответствии R = <X,Y,G_R>, где G_R 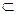X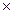Y все пары вида (a; у), где 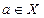и 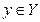, для которых верно аRу.

Множество всех таких у из множества Y, для которых верно аRy, назовём полным образом элемента а Х в соответствии R между элементами множеств Х и Y.

X Y

Y₁

Y₂

Y₃

Пусть у=bY. Расмотрим все пары вида (х,b) для которых верно хRb. Тогда множество таких х из множества Х, для которых верно хRb, назовём полным прообразом элемента b соответствии R между элементами множеств Х и Y.

X Y

X₁

X₂

X₃

X₄

В примере 1 полный прообраз элемента 4 состоит из одного элемента: 2; полный образ элемента 3 состоит из одного элемента: 9.

Способы задания соответствий

1) по определению бинарное соответствие будет задано, если будут заданы множества Х,Y, и G_R - это самый общий способ задания cоответствия;

2) соответствие может быть задано своим графиком: G_R = {(x,у)| хХ, уR,хRy}. График соответствия может быть задан перечислением элементов или указанием характеристических свойств;.

3) если множества Х и Y конечные, то соответствие между элементами этих множеств может быть задано с помощью графа:

X R Y

4) с помощью таблицы, если множества Х и Y-конечные;

Х У

5) соответствие может быть задано графически на плоскости, если множества Х и Y -числовые.

В примере 1

9 М₂ М₁ (2;4).

М₂(3;9).

4 М₁

2 3 5

6) с помощью двухместного предиката, то есть предложения с двумя переменными, выражающего факт вступления элементов в соответствие.

R(х; у): хRy, хХ, у Y

R(x; у): «x – делитель y», х Х, у Y.

Рассмотрим между элементами множеств Х = {2; 3; 4} и Y = {5; 6; 8} соответствие R: х - делитель у. Тогда Х - область отправления соответствия, Y - область прибытия. Область определения соответствия: Д_R = {2,3,4}, множество значений соответствия: Е_R = {6;8 }.

Пусть соответствие между элементами множеств X и Y задано при помощи графа.

X R Y

.

Тогда полный образ элемента 2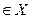состоит из двух элементов: 6 и 8:

R(2) = {6;8}; R(3) = {6}; R(4) = {8}. R(7) – пуст.

Полный прообраз элемента 5 пуст; ; .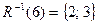

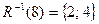Дата добавления: 2014-01-11