
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства отношений на множестве
|
|
|
|
Пусть F=<X, X, GF >, где GF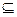 X2 – отношение на множестве Х.
X2 – отношение на множестве Х.
GF = {(x,y)| x X, y
X, y X, xFy}.
X, xFy}.
Определение: Отношение на множестве Х называется рефлексивным, если всякий элемент x X вступает в это отношение сам с собой:
X вступает в это отношение сам с собой:
(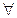 x
x X) [xFx]- «и»
X) [xFx]- «и»
Особенности графа: в каждой вершине графа рефлексивного на множестве Х отношения - петля.
Особенности графика: графику рефлексивного отношения принадлежат все пары вида (х,х): (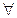 x
x X) (x; x)
X) (x; x)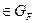 .
.
Определение 2: Отношение F на множестве Х называется антирефлексивным, если ни один элемент множества Х не вступает в отношения F сам с собою:
(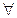 х
х Х)[
Х)[  ]-«и».
]-«и».
Особенности графа: ни в одной вершине графа нет петли.
Особенности графика: графику не принадлежит ни одна пара с равными компанентами (вида (х,х)): (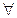 x
x X) (x; x)
X) (x; x)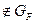 .
.
Примеры: отношение равенства на множестве множеств; не меньше; не больше на числовом множестве; параллельности на множестве прямых и т.д. – рефлексивные отношения. Отношения неравенства; больше; меньше на числовых множествах; перпендикулярности на множестве прямых и др. – антирефлексивные отношения.
Рассмотрим отношение, заданное на множестве людей: «быть отцом».
Является ли оно рефлексивным? Нет, так как ни один человек не может быть отцом самому себе. Стало быть, оно антирефлексивное.
Определение 3: Отношение F на множестве Х называется симметричным, если для любых элементов х,у Х истинно утверждение: если элемент x вступил в отношение F c элементом y (хFy), то и элемент y вступил в данное отношение с элементом x (уFx):(
Х истинно утверждение: если элемент x вступил в отношение F c элементом y (хFy), то и элемент y вступил в данное отношение с элементом x (уFx):(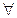 х,у
х,у Х)[xFy
Х)[xFy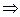 yFx] – «и».
yFx] – «и».
Особенности графа: граф симметричного отношения содержит только двойные стрелки или никаких.
Особенности графика: если графику принадлежит пара (х,у), то и пара (у,х) принадлежат этому графику: (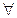 x,y
x,y X) [(х,у)
X) [(х,у) GF
GF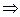 (y,x)
(y,x) GF].
GF].
Примеры: отношения равенства на множестве множеств и на числовом множестве; отношения параллельности и перпендикулярности на множестве прямых; отношение «быть родственником» на множестве людей и др.
Определение 4: Отношение F на множестве Х называется асимметричным, если для любых двух элементов х и у множества Х верно утверждение: если элемент х X вступает в отношение F с элементом у, то неверно, что элемент у вступает в отношение F c элементом х этого же множества: (
X вступает в отношение F с элементом у, то неверно, что элемент у вступает в отношение F c элементом х этого же множества: (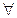 x,y
x,y X) [xFy
X) [xFy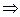
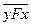 ]-«и».
]-«и».
Другими словами: ни для каких элементов х и у  Х; не может быть одновременно xFy u yFx.
Х; не может быть одновременно xFy u yFx.
Особенности графа: все стрелки графа асимметричного отношения одинарные и ни в одной вершине нет петель!
Особенности графика: (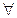 x,y
x,y X) если (х,у)
X) если (х,у) GF, то (у,х)
GF, то (у,х)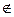 GF.
GF.
Примеры: отношения «>»; «<»; «толще» и т.д. являются асимметричными.
Определение 5: Отношение F на множестве Х называется антисимметричными, если для любых двух различных элементов х и у из множества Х истинно утверждение: если х Х вступает в отношение F с элементом у, то у не вступает в отношение F с элементом х.
Х вступает в отношение F с элементом у, то у не вступает в отношение F с элементом х.
Итак, F - антисимметрично 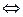 (
(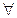 x,y
x,y X) (x ≠ y) [xFy=>
X) (x ≠ y) [xFy=>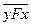 ].
].
Особенности графа: граф антисимметричного отношения содержит только одинарные стрелки и могут быть петли.
Особенности графика: (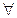 x,y
x,y X) если (x,y)
X) если (x,y) GF, то (у,х)
GF, то (у,х)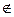 GF, и (x,x)
GF, и (x,x) GF
GF
Замечание: асимметричное отношение - это одновременно антисимметричное и антирефлексивное отношение.
Определение 6: Отношение F на множестве Х называется транзитивным, если для любых трех элементов множества Х справедливо утверждение: если элемент х находится в отношении F с элементом y, а элемент y находится в отношении F с элементом z, то элемент х вступит в отношение F с элементом z: (xFy)Λ(yFz)=>(xFz).
Таким образом, F – транзитивно 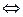 (
(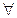 x,y,z
x,y,z X)[xFy
X)[xFy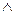 yFz
yFz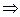 xFz].
xFz].
Особенности графа: граф транзитивного отношения с каждой парой стрелок идущих от х к у и от у к z, содержит стрелку от х к z.
Особенности графика: если (x,y) GF
GF 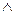 (y,z)
(y,z) GF то (х,z)
GF то (х,z) GF.
GF.
Пример 1: отношение параллельности на множестве прямых является транзитивным: (a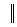 в)
в)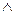 (в
(в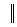 с)
с)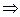 (a
(a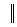 c) для любых (
c) для любых (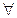 a,в,с) из множества прямых на плоскости.
a,в,с) из множества прямых на плоскости.
Пример 2: отношение «>» на множестве действительных чисел:
(х > y)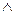 (y > z)
(y > z)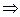 (x > z)(
(x > z)(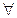 x,y,z
x,y,z R).
R).
Определение 7: Отношение F на множестве Х называется антитранзитивным, если для (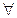 х,у,z
х,у,z X) верно утверждение: если элемент х находится в отношении F с элементом y, а элемент y находится в отношении F с элементом z, то элемент х не вступает в отношение F с элементом z: [xFy
X) верно утверждение: если элемент х находится в отношении F с элементом y, а элемент y находится в отношении F с элементом z, то элемент х не вступает в отношение F с элементом z: [xFy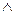 yFz=>
yFz=>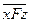 ].
].
Таким образом, F - антитранзитивно 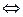 (
(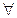 x,y,z
x,y,z X)[xFy
X)[xFy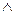 yFz=>
yFz=>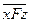 ].
].
Особенности графа: если граф содержит стрелку от х к у и у к z, то не содержит стрелку от х к z.
Особенности графика: если (x,y) GF
GF 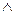 (y,z)
(y,z) GF то (х,z)
GF то (х,z)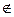 GF.
GF.
Пример 1: отношение перпендикулярности на множестве прямых антитранзитивно.
 а
а
 |
 в с
в с

Определение 8: Отношение F на множестве Х называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Пример: отношение равенства на множестве чисел, отношение параллельности на множестве прямых, отношение равенства на множестве множеств, отношение подобия на множестве фигур являются отношениями эквивалентности.
Отношение эквивалентности связано с разбиением множества на классы.
Теорема: Для того, чтобы отношение R позволяло разбить множество X на попарно непересекающиеся классы, необходимо и достаточно, чтобы R было отношением эквивалентности.
Доказательство смотри стр 174 учебника ч.1 (Охременко Д.В., Тонких А.П.)
Пример: Пусть X = {x ׀ x N, x < 12}. Зададим отношение F: x и у делятся на 5 с одинаковым остатком.
N, x < 12}. Зададим отношение F: x и у делятся на 5 с одинаковым остатком.
Является ли оно отношением эквивалентности? Если да, то задайте классы эквивалентности. Укажите граф.
Данное отношение рефлексивно, симметрично, транзитивно. Следовательно, оно является отношением эквивалентности и производит разбиение множества Х на классы эквивалентности.
1:5=0(ост.1) 6:5=1(ост.1) 11:5=2(ост.1)
2:5=0(ост.2) 7:5=1(ост.2)
3:5=0(ост.3) 8:5=1(ост.3)
4:5=0(ост.4) 9:5=1(ост.4)
5:5=1(ост.0) 10:5=2(ост.0)
Тогда Х 1 = {1,6,11} X 2 = {2,7} X 3 = {3,8} X 4 = {4,9} X 5 = {5,10}.
Все условия разбиения множества на классы выполнены:
X i Xj = Ǿ (
Xj = Ǿ (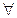 i,j
i,j N) X1
N) X1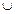 X2
X2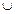 X3
X3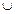 X4
X4 X5 = X.
X5 = X.
 | |||
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2330; Нарушение авторских прав?; Мы поможем в написании вашей работы!