Отношение многие-ко-многим

На рис. 2.5 показаны таблицы, состоящие в отношении многие-ко-многим. Каждой учебной группе соответствует несколько преподавателей. Каждый преподаватель мо­жет вести, во-первых, несколько разных предметов и, во-вторых, преподавать в раз­ных группах.

Таблица «Учебные группы Таблица

и дисциплины» «Преподаватели»

Рис. 2.5. Связь многие-ко-многим

Некоторые СУБД не поддерживают связи многие-ко-многим на уровне индексов и ссылочной целостности (см. следующий подраздел), хотя и позволяют реализовывать ее в таблицах неявным образом. Считается, что БД всегда можно перестроить так, чтобы любая связь многие-ко-многим была заменена на одну или более связей один-ко-многим.

5. Реляционная алгебра отношений: атрибуты, домены, отношения, схемы атрибутов. Ключи и суперключи. Реляционные операторы: объедение, пересечение, проекции, выборки, декартово произведение, соединения, деление отношений.

Теоретической основой манипулирования данными является реляционная алгебра. Конечно, в реализациях конкретных реляционных СУБД сейчас не используется в чистом виде ни реляционная алгебра, ни реляционное исчисление. Фактическим стандартом доступа к реляционным данным стал язык SQL (Structured Query Language). Язык SQL представляет собой смесь операторов реляционной алгебры и выражений реляционного исчисления, использующий синтаксис, близкий к фразам английского языка и расширенный дополнительными возможностями, отсутствующими в реляционной алгебре и реляционном исчислении. Вообще, язык доступа к данным называется реляционно полным, если он по выразительной силе не уступает реляционной алгебре (или, что то же самое, реляционному исчислению), т.е. любой оператор реляционной алгебры может быть выражен средствами этого языка.

Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов, и возвращающие отношения в качестве результата. Таким образом, реляционный оператор выглядит как функция с отношениями в качестве аргументов:

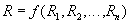
Реляционная алгебра является замкнутой, т.к. в качестве аргументов в реляционные операторы можно подставлять другие реляционные операторы, подходящие по типу, например,

R=f (f_1 (R_11,R_12,…), f_2(R_21,R_22,…))

Таким образом, в реляционных выражениях можно использовать вложенные выражения сколь угодно сложной структуры. Каждое отношение обязано иметь уникальное имя в пределах базы данных. Имя отношения, полученного в результате выполнения реляционной операции, определяется в левой части равенства. Однако можно не требовать наличия имен от отношений, полученных в результате реляционных выражений, если эти отношения подставляются в качестве аргументов в другие реляционные выражения. Такие отношения будем называть неименованными отношениями. Неименованные отношения реально не существуют в базе данных, а только вычисляются в момент вычисления значения реляционного оператора. Традиционно, вслед за Коддом [43], определяют восемь реляционных операторов, объединенных в две группы.

Теоретико-множественные операторы:

• Объединение
• Пересечение
• Вычитание

· Декартово произведение

Специальные реляционные операторы:

• Выборка
• Проекция
• Соединение
• Деление

Не все они являются независимыми, т.е. некоторые из этих операторов могут быть выражены через другие реляционные операторы.

Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.

Определение 1. Будем называть отношения совместимыми по типу, если они имеют идентичные заголовки, а именно,

• Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении,
• Атрибуты с одинаковыми именами определены на одних и тех же доменах.

Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.

Дата добавления: 2014-01-11