Принцип эквивалентности для циклических процессов

Рассмотрим циклический процесс, который совершается с помощью устройства, схема которого приведена на рис.2. Оно состоит из поршня с цилиндром, который погружен в термостат с водой. Предположим, что в цилиндре находится один моль идеального газа. Температуру воды можно очень плавно без резких скачков повышать или понижать, используя нагревательные или охладительные устройства.

Т₂ V₂ P₂

Т₁ V₁ P₁

Рис.2 Схема устройства теплоты и работы в циклическом процессе

Источник теплоты и холодильный элемент устроены таким образом, что позволяют точно определять количество теплоты, которая подводится к системе (газ + вода в термостате) и отводится от системы. Вода в термостате постоянно перемешивается мешалкой, чтобы исключить перепады температуры в разных частях термостата. Только в этом случае температура Т₁ будет иметь смысл физического параметра в целом для воды в термостате и для газа в цилиндре.

Условимся также, что между поршнем и цилиндром отсутствуют силы трения.

С помощью термостата будем медленно нагревать воду. Через некоторый промежуток времени объем газа увеличиться с V₁ до V₂ с одновременным повышением температуры с Т₁ до Т₂^*. При этом будет произведена объемная работа по преодолению внешних сил.

(6)

Из сущности процесса следует, что Р_внеш равно давлению газа, Р_внеш = Р_г.

Из сравнения объемной работы, вычисляемой по уравнению () с теплотой, подведенной к системе, можно обнаружить, что последняя величина превышает полученную работу, Q > W. Это несовпадение, очевидно, связано с повышением температуры газа и воды в термостате с Т₁ до Т₂.

Под действием теплоты изменяется состояние газа и воды в термостате и на это затрачивается часть теплоты (в следующем разделе будет показано, что теплота расходуется на увеличение внутренней энергии газа и воды в термостате). Проведем процесс в обратном направлении. Для этого соединим систему с холодильником, температура которого несколько ниже температуры системы Т₁. В этом случае под действием внешнего давления при минимальном градиенте температур между холодильником и системой на каждом этапе охлаждения, совершается работа сжатия газа

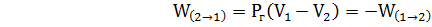(7)

________________________

*При постоянном давлении имеем

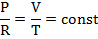
Температура возрастает во столько же раз во сколько увеличивается объем

и постепенное понижение температуры с Т₂ до Т₁. Холодильное устройство полностью поглощает теплоту, выделяющуюся при совершении работы сжатия. Очевидно также, что при условии Р_внеш = Р_г работа сжатия, взятая с обратным знаком, равна работе расширения. Поэтому для проведенного циклического процесса можно написать

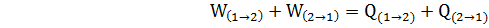(8)

где символы «1→2» и «2→1» обозначают процессы в прямом и обратном направлениях.

В соотношении (8) слагаемые, связанные с изменениями состояния системы в 1→2 и 2→1процессах взаимно погашаются, что и обеспечивает выполнимость закона эквивалентности.

Взаимная компенсация энергетических изменений в системе возможна только в циклических процессах и это обстоятельство объясняет, почему закон эквивалентности в общем случае выполняется только для циклических процессов.

Для произвольного циклического процесса имеем

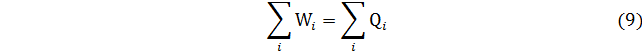
В уравнении ()– сумма всех работ, которые совершает система, и которые совершаются средой над системой. Аналогично, – сумма теплот, которые переходят от внешней среды к системе и от системы к внешней среде.

Закон эквивалентности справедлив для любых процессов, поскольку в его основе лежит закон сохранения энергии, которой, в форме теплоты и работы, обмениваются между собой система и окружающая среда. Действительно, пусть система (в рассмотренном случае идеальный газ + вода в термостате) в конце циклического процесса не вернулась в исходное состояние. Иными словами, температура системы или какой-то другой параметр, связанный с работой допустим давление, имели значение более высокое, чем в начале процесса. Это означает, что система в результате циклического процесса накопила избыточную энергию, возникшую из ничего. Не согласуется с законом сохранения энергии предположение, что параметры системы в конце циклического процесса ниже, чем в исходном состоянии. В этом случае в окружающую среду поступает больше энергии, также возникшей из ничего. Поэтому единственное заключение, которое можно сделать из этих рассуждений, состоит в том, что система в любом циклическом процессе возвращается в исходное состояние.

Теперь предположим, что 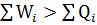. Из этого следует, что в циклическом процессе получено дополнительное количество теплоты, источники которой неизвестны. Другими словами она создается, что противоречит закону сохранения энергии. Неравенство означает, что избыточная работа совершается за счет энергии не существующего источника, что также не согласуется с законом сохранения энергии. Из проведенного рассмотрения следует, что для произвольного циклического процесса работа эквивалентна теплоте, поскольку только это соотношение находится в согласии с законом сохранения энергии.

Процессы, которые использовали Майер и Джоуль для определения механического эквивалента теплоты, естественно, удовлетворяли условию цикличности. В описанном выше опыте Джоуля (рис.1) он состоял из двух стадий: стадии, где совершается работа над системой падающим грузом, и стадии теплоотдачи при охлаждении системы до первоначальной температуры. Количество выделяющейся в окружающую среду теплоты при охлаждении системы Джоуль определял по градуировочному графику.

РАЗДЕЛ 3. Математическое выражение первого закона термодинамики

Для нециклических процессов Q – W ≠ 0. Обозначим эту разность величиной ∆U.

Для процесса, схема которого изображена на рис.2 раздела 2, разность между теплотой и работой системы, как раз и равна ∆U. Величина U носит название внутренней энергии.

Для любого произвольного процесса, который совершается при взаимодействии системы с окружающей средой, имеем

Q – W = ∆U (1)

Обычно уравнение (1) представляют в таком виде

Q = ∆U + W (2)

Это и есть математическое выражение первого закона термодинамики (в интегральной форме). С учетом знаков Q и W его можно выразить следующим образом: теплота, которая переходит от окружающей среды к системе, расходуется на увеличение внутренней энергии системы и на совершение работы системой над средой. В уравнении (2) величина W – сумма всех физически возможных работ, например, объемная, электрическая и другие.

Выясним некоторые особенности внутренней энергии, как физической величины.

Предположим, что система может переходить из состояния 1 в состояние 2 двумя путями а и в, в обратном направлении 2→1 по пути с.

Пусть система переходит из состояния 1 в состояние 2 по пути а, а возвращается в исходное состояние по пути с. Система совершила циклический процесс 1 – а – 2 – с – 1.

На пути 1 – а – 2 в соответствии с уравнением (2) имеем

Аналогично для пути 2 – с – 1 можно написать

В целом для циклического процесса

Но для циклического процесса

Из последнего соотношения следует

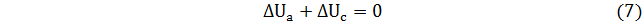
В циклическом процессе суммарное изменение внутренней энергии равно нулю, поскольку ∆U в прямом 1→2 процессе равно изменению ∆U (с противоположным знаком) в обратном процессе 2→1.

В конце циклического процесса внутренняя энергия имеет такое же значение, какое она имела в начале процесса. Из этого свойства внутренней энергии следует, в частности, невозможность построения вечного двигателя.

Далее рассмотрим процесс по пути 1 – в – 2 – с.

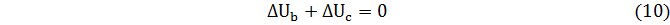
Из сравнения уравнений (8) и (10) следует еще один важный вывод

Изменение внутренней энергии в любом произвольном процессе не зависит от его пути. Оно однозначно определяется значением внутренней энергии системы в конце и вначале процесса

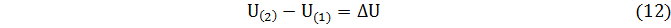
Такая особенность характерна для любого вида энергии. Физические величины, изменение которых не зависит от пути процесса, называются свойствами системы.

Свойствами системы являются такие термодинамические величины как энтальпия (Н), энтропия (S), энергия Гиббса (G), энергия Гельмгольца (А), физические величины, такие как масса вещества, объем, давление, температура и ряд других. Все они обладают одной общей особенностью – их изменение зависит только от их значений в конце и начале процесса и не зависит от того, каким образом совершается (физически или мысленно) это изменение. В общем случае, обозначая свойство системы ψ, для процесса 1→2

Рассмотрим такой пример. Пусть имеется раствор двух веществ с объемом V₁. Предположим, что далее произошло уменьшение объема до значения V₂. Очевидно, что ∆V = V₂ – V и оно не зависит от того каким собственно способом происходило это изменение.

Из выражения (13) следует, что само значение как физико-термодинамической величины зависит от параметров системы, оно определяется исключительно этими параметрами. Например, U, H и S и другие свойства чистого вещества в любом агрегатном состоянии зависят от двух параметров, например, T и Р

Если например Р = const

С математической точки зрения свойство системы является функцией параметров системы, определяющих ее состояние. Поэтому вместо термина свойство системы обычно применяют выражение – функция состояния. Например, для чистого вещества, используя в качестве параметров состояния Т, Р можно написать

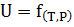
Из сказанного следует, что дифференциальной формой свойства системы является полный дифференциал dU.

Для одного моля идеального газа

Тогда в соответствии с теоремой о полном дифференциале имеем

В качестве свойства системы можно использовать и температуру. Тогда

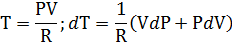
В отличие от энергии работа и теплота не являются свойствами системы. Их количество зависит не только от параметров системы в конце и начале процесса, но и от того как происходил процесс, от его пути. По этой причине их называют функциями пути. Энергия связана с процессом через ее изменение, а теплота и работа с их количеством в процессе.

Дифференциальной формой теплоты и работы является неполный дифференциал.

Их обозначают соответственно δQ и δW. Математические особенности полного и неполного дифференциала рассматриваются в разделе 4.

С учетом особенностей дифференциальных форм внутренней энергии, теплоты и работы первый закон термодинамики можно записать в следующем виде

В физико-химических процессах важную роль играет объемная работа

Все другие виды работ будем обозначать 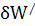. Работу 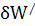часто называют полезной работой.

Тогда

(15)

В термодинамике важную роль играет свойство системы, называемое энтальпией

(16)

где, Р – давление системы, V – объем системы.

Произведение PV имеет размерность энергии, но ему достаточно сложно придать точный физический смысл.

Для дифференциала Н имеем

Подставляя выражение для d U, которое следует из уравнения (17), в уравнение (15) находим

Для обычных физико-химических процессов единственным видом работы является объемная работа, 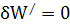. В этом случае имеем

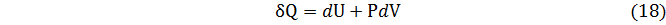
Дата добавления: 2014-01-11