Автокаталитические реакции

Реакция называется автокаталитической, если она ускоряется одним из продуктов реакции. Примером автокатализа является окисление щавелевой кислоты перманганатом. Тут катализирующим действием обладает продукт реакции ион двухвалентного марганца. Первой стадией реакции является взаимодействие перманганат-иона с ионом марганца (2+):

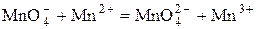
Эта стадия протекает медленно, то есть является лимитирующей.

Далее трехвалентный ион марганца реагирует с щавелевой кислотой с образованием двуокиси углерода и иона двухвалентного марганца:

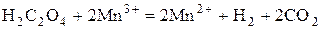
Эта реакция протекает быстро.

В общем виде механизм автокаталитической реакции можно представить схемой:

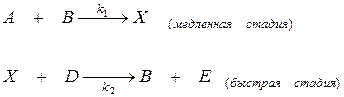
Так как скорость реакции определяется первой лимитирующей стадией, то можно записать, что общая скорость равна:

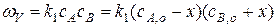
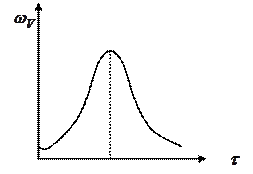Реакция начинается с очень низкой скоростью, но по мере накопления B скорость реакции возрастает и достигает максимума. Достигнув максимума скорость реакции уменьшается за счет снижения концентрации реагента А.

Одной из общих характеристик таких реакций, протекающих в закрытых системах является наличие максимума на кривой зависимости скорости реакции от времени и наличие индукционного периода.

Зависимость скорости автокаталитической реакции от времени

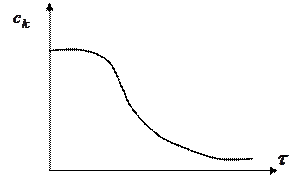
Зависимость концентрации исходного вещества от времени

Период времени, когда реакция не протекает, называется периодом индукции. Автокаталитические реакции рассматриваются не в разделе катализа, так как тут нарушается одно из основных признаков катализа - постоянство концентрации катализатора, ее неизменность к концу каталитического акта.

В присутствии некоторых веществ скорость реакции может не возрастать, а напротив,уменьшаеться. Такое явление получило название ингибирования, а вещества, замедляющие скорость реакции называются ингибиторами. Сущность явления ингибирования состоит в том, что игибитор вступает в химическое взаимодействие в реагентом или чаще вс промежуточными веществами с образованием устоячивых соединений, облажающих низкой реакционной способностью. Например, ингибиторы применяются для снижения деструкции полимерных материалов, протекающих под действием теплоты и УФ-излучения.

Рассмотрим в общем виде два случая:

1. когда вещество, являющееся продуктом реакции находится в следовых количествах изначально в системе:

2. когда этого вещества в начале нет, но оно постепенно накапливается в системе.

Первому случаю соответствует схема:

A ® B

Причем 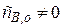. Это так называемый «метод затравки», так как количество продукта очень мало: .

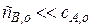Дифференциальное кинетическое уравнение будет иметь вид:

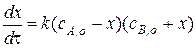
Второму случаю соответствует схема

,

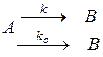Т.е. одна стадия является каталитической (константа скорости ее k), а вторая некаталитической (с константой скорости k _o), причем очевидно, что k _o<< k.

Кинетика каталитической реакции описывается уравнением

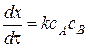
Некаталитической стадии: .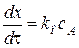

Дифференциальное кинетическое уравнение всего процесса в этом случае будет иметь вид:

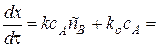
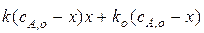
Или после преобразования

.

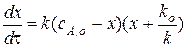Очевидно, что .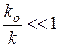

Сравнивая конечные дифференциальные уравнения в обоих случаях приходим к выводу, что они идентичны, причем и 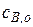(затравка) и 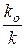- очень маленькие величины.

Стационарное и квазистационарное протекание реакций. Метод квазистационарных концентраций Боденштейна.

Как было показано ранее для кинетического описания даже простейшей двустадийной односторонней реакции, протекающей в закрытой системе приходится решать систему дифференциальных уравнений. Если число стадий превышает две, некоторые из них являются двусторонними, би и тримолекулярными, то математические выражения усложняются настолько, что решение нельзя получить в аналитическом виде. Однако, для определенных типов реакций в определенных условиях процесс может протекать в стацонарном режиме и тогда кинетические расчеты существенно упрощаются.

Стационарный режим может установиться в открытой системе, при этом концентрации промежуточных веществ в данной точке пространства остаются постоянными. А это означает, что скорости образования и расходования промежуточных веществ одинаковы., то есть

.

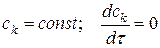Для закрытых систем в некоторых случаях можно ввести понятие квазистационарного режима.

Рассмотрим двухстадийную последовательную реакцию

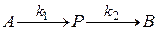
Если 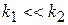, то после 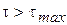, раз

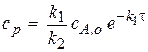
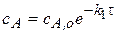
то отношение 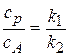= const.

С течением времени отношение концентрации промежуточного вещества и исходного не изменяется, и говорят, что реакция протекает в квазистационарном режиме. В таких случаях можно выразить концентрацию промежуточного вещества через концентрацию исходного реагента и исключить ее из системы дифференциальных уравнений. Это весьма полезно, так как концентрацию промежуточного вещества обычно трудно определить, а теперь в системе уравнений остаются лишь аналитически определяемые концентрации.

Это существенно облегчает анализ кинетической кривой и является сутью метода квазистационарных концентраций Боденштейна.

Рассмотрим последовательную реакцию

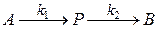
к которой можно применить принцип квазистационарности, то есть константа скорости 2 стадии гораздо больше константы скорости первой стадии.

Метод квазистационарных концентраций Боденштейна основан на том, что разность скоростей образования промежуточного вещества и его расходования (то есть плотность скорости изменения числа молей промежуточного вещества) мала по сравнению с самими скоростями образования и расходования промежуточных веществ и может быть приравнена к нулю

То есть выразив скорость реакции как скорость накопления промежуточного вещества, мы можем приравнять ее нулю.

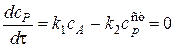
Рассмотрим систему с протекающей в ней последовательной реакцией, которую можно представить следующей схемой

1 стадия: прямая реакция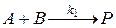

обратная реакция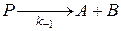

2 стадия: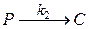

Известно, что .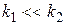

Запишем дифференциальное уравнение для скорости образования промежуточного вещества. Промежуточное вещество накапливается по прямой реакции 1 стадии и расходуется по обратной реакции первой стадии и по второй стадии. Применим условие стационарности.

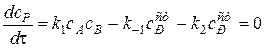
Отсюда легко выразить концентрацию промежуточного вещества

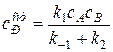
а затем привлечь ее в выражение для скорости накопления продукта реакции

w _V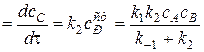

Сложное соотношение констант скоростей можно представит как эффективную константу скорости:

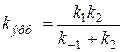
Тогда закон скорости будет иметь вид:

w _V =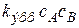

Формально реакция в квазистационарном режиме описывается уравнением второго порядка, причем константа скорости представляет собой сложный комплекс констант скоростей стадий, и определить их при таком допущении по экспериментальным данным по отдельности невозможно. То есть при использовании квазистационарного приближения с одной стороны упрощается описание кинетики, а с другой - теряется информация о константах элементарных стадий.

Следует иметь в виду, что для установления квазистационарного режима необходимо определенное время с начала реакции, обозначим его 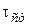. Величину 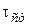можно определить из условия:

,

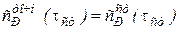В котором

,

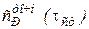
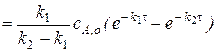а = .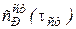

Решая находим:

. ,

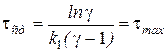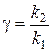Т.е. время достижения максимума концентрации промежуточного вещества можно приравнять времени установления квазистационарного режима.

Дата добавления: 2014-01-11