Расчет на контактную прочность активных поверхностей зубьев

Расчет на контактную прочность активных поверхностей зубьев является основным для закрытых (работающих в масле) передач.

Экспериментально установлено, что наименьшую контактную прочность имеет околополюсная зона активных (рабочих) поверхностей зубьев. Поэтому расчет контактных напряжений производят для фазы контакта зубьев в полюсе зацепления (рис. 20.32).

Прямозубые и косозубые передачи. В расчете полагают, что контакт двух зубьев аналогичен контакту двух цилинд­ров с радиусами p₁ и р₂, равными радиусам кривизны эвольвент зубьев в точке контакта, т. е. для расчета зубьев используется задача Герца о контакте цилиндров (см. гл. 14). Использование такой модели оказывается оправданным, так как размеры площадки контакта малы по сравнению с раз­мерами зуба.

Максимальное контактное напряжение 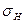в зоне контакта зубьев можно вычислить по формуле (19.3) при q = w_n.

Для получения расчетного соотношения выразим величины, входящие в равенство (19.3), через силовые и геометриче­ские параметры передачи.

Нормальное удельное усилие w_n связано с расчетной удельной окружной силой зависимостью [см. формулу (20.20)]*

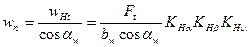(20.28)

……………………………..

* Здесь и далее параметрам, связанным с расчетом контактной проч­ности передач, приписывается индекс Н.

Сначала рассмотрим расчет косозубой передачи. Радиусы кривизны для косозубого зацепления находим по диаметрам эквивалентных прямозубых колес (см. с. 334)

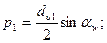
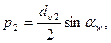
тогда, имея в виду передаточное число и = d₂/d_{1 ,}

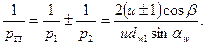
Знак плюс берется при расчете внешнего зацепления, а знак минус — внутреннего.

Учитывая эти соотношения и зависимость (19.3), запишем условие контактной прочности по допускаемым напряжениям для активных поверхностей зубьев

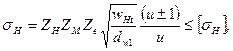(20.29)

где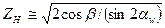— коэффициент, учитывающий форму сопряженных поверхностей, 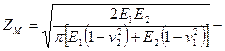коэффициент, учитывающий механические свойства материалов колес (модули упругости E₁ и Е₂ и коэффициенты Пуассона v₁ и v₂), для стальных колес Z_M = 275 МПа^1/2; Z_e - коэф­фициент, учитывающий суммарную длину контактных линий; для прямозубых колес Z_e = 1; для косозубых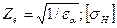— допускаемое напряжение (см. ниже с. 359).

Расчетные напряжения 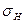одинаковы для обоих колес, поэтому расчет выполняют для того из колес пары, у кото­рого допускаемое напряжение 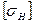меньше.

Менее прочным часто бывает колесо, тогда для него и ведут расчет на прочность.

Подставляя в условие (20.29) соотношение для w_Ht и при­нимая 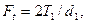а также 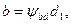после простых преоб­разований получим

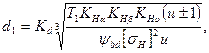(20.30)

где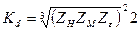— коэффициент.

В предварительных расчетах для стальных прямозубых колес можно принимать

K_d = 770 МПа^1/3, для косозубых колес K_d = 680 МПа^1/3, 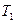— вращающий момент на шестерне, Н• м; 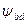— коэффициент ширины колеса: для колес малой твердости (НВ < 350) принимают 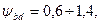при их кон­сольном расположении 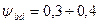; для колес высокой твер­дости (НВ > 350) принимают 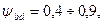при их консоль­ном расположении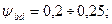

и — передаточное число.

Значения 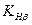можно принимать из табл. 20.1; в пред­варительных расчетах можно считать.

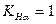Из формулы (20.30) видно, что размер колес (габариты) из условия контактной прочности не зависит от модуля (размеров зуба). Это объясняется тем, что размеры площадки контакта малы в сравнении с размерами зуба. Габариты передачи в этом случае можно уменьшить за счет повы­шения прочности поверхностных слоев зубьев (увеличением 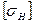) путем поверхностной закалки или химико-термической обработки, увеличением приведенного радиуса кривизны точек зубьев путем изготовления колес с положительным смещением х, а также увеличением межосевого расстояния.

В практических расчетах минимальное значение модуля устанавливают из расчета на изгиб. Если оказывается, что расчетное значение m < 1,5 мм, то принимают 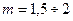мм, так как при малом значении т возрастают требования к жесткости передачи, увеличивается опасность повреждения зубьев из-за концентрации нагрузки и в связи с перегрузкой.

Далее при известном модуле определяют остальные размеры передачи:

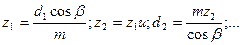
Отметим, что должно быть z₁ > z_min, где z_min — минимальное число зубьев; z_lmin 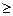17

(см. с. 331).

Расчет прямозубых колес ведут по тем же формулам при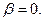

Конические передачи. Для прямозубого конического зацеп­ления приведенный радиус кривизны р_п определяют по ди­аметрам эквивалентных колес [см. с. 337]

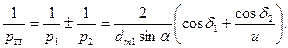
Принимая во внимание, что 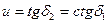, получим

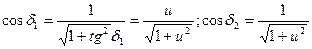
После подстановки и несложных преобразований имеем

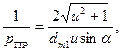
где d_m1 — средний диаметр меньшего колеса (шестерни).

Удельная нагрузка в этом сечении определяется так же, как и для прямозубого колеса.

Учитывая эти соображения, из условия прочности по допускаемым контактным напряжениям несложно получить следующее соотношение, аналогичное формуле (20.30):

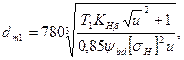(20.31)

где 0,85 — экспериментальный коэффициент;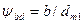— ко­эффициент ширины шестерни относительно диаметра d_m1 обычно 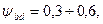меньшие значения берут для колеса с высокой твердостью зубьев (НВ > 350).

Далее расчет ведут в той же последовательности, как и расчет цилиндрических передач.

Дата добавления: 2014-01-11