
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плоские кривые линии
|
|
|
|
Среди плоских алгебраических кривых особо следует отметить кривые второго порядка.
Эти кривые иногда рассматривают как плоские сечения поверхностей - “конические сечения”.
Рассмотрим три простейших канонических формы: эллипс, гиперболу и параболу.
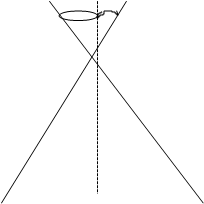
Зададимся конической поверхностью.
 |
Т
 Y
Y
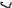 j Г 1
j Г 1



 y
y

 Эллипс
Эллипс
 х F1· о F2·
х F1· о F2·
· М
 Окружность Г 2
Окружность Г 2
 | |||
 |
1. Эллипс - j > y 2. Окружность - j = 90 град.
Эллипс геометрическое место точек М, сумма расстояний которых до двух заданных точек (F1, F2) называемых фокусами, есть величина постоянная.
Рассечем коническую поверхность плоскостью Г2 параллельной образующей конуса и не проходящей через вершину Т:



 Г 1
Г 1

 Г 2
Г 2
Т
Парабола - j = y
 | |||||
 | |||||
 |
y
 |
 Двойная прямая
Двойная прямая
- Г 1 É Т j
 |
Для получения гиперболы коническую поверхность необходимо рассечь плоскостью Г2 не проходящей через вершину конуса и не параллельную его образующей.
 |
 Г 1 Г 2
Г 1 Г 2
Т

 Две пересекающиеся прямые - Гипербола -
Две пересекающиеся прямые - Гипербола -
Г 1 É Т. j < y.
 |
См. Л. с. 128 - 129.
Прямая линия и ее задание на комплексном чертеже.
Прямая линия - это простейший представитель семейства линий.
На комплексном чертеже прямая линия может быть задана непосредственно своими проекциями, проекциями двух точек принадлежащих прямой или следами.
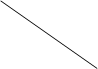
При ортогональном проецировании на плоскость, не перпендикулярную ей, прямая проецируется в прямую линию.
Чтобы спроецировать отрезок прямой линии АВ на плоскость, из крайних точек отрезка опускают перпендикуляры на плоскость проекций и полученные проекции точек А1 и В 1 соединяют прямой которяй и будет проекцией данного отрезка.


 Z
Z
П 2 В 2










 Т В
Т В
А2




 А 1 2 90
А 1 2 90


 1
1




 Х Ах В х
Х Ах В х

 А1 90
А1 90
 |
 В 1 П 1
В 1 П 1
 |
Y
Одна проекция прямой не определяет ее положение в пространстве, так как может соответствовать множеству прямых расположенных в этой же проецирующей плоскости.
Необходимо иметь не менее двух проекций отрезка прямой, чтобы определить положение прямой в пространстве.
Отрезок АВ наклонен ко всем плоскостям проекций, поэтому проекции отрезка будут меньше его самого. Прямая наклоненная ко всем плоскостям проекций, называется прямой общего положения.
Рассмотрим прямоугольный треугольник D АВ1. Горизонтальная проекция
çА 1, В 1ç будет равна катету А,1 этого треугольника.
Чтобы определить величину второго катета В, 1 посмотрим на фронтальную плоскость проекций. Проекция на фронтальную плоскость В 2, 1 2 равна натуральной величине второго катета В, 1. Мы в этом дополнительно убедимся когда рассмотрим частное положение прямых в пространстве. Сейчас забегая вперед, я хочу обратить ваше внимание, что катет В,1 перпендикулярен горизонтальной плоскости проекций и параллелен фронтальной плоскости проекций.
Таким образом, зная два катета прямоугольного треугольника, мы можем найти его гипотенузу. Имея комплексный чертеж прямой общего пложения, где ни одна из проекций отрезка этой прямой не равна натуральной величине отрезка, мы всё
же можем найти его натуральную величину.
В 2


 )
)

 А 2 1 2
А 2 1 2
 Х А х
Х А х
 А 1
А 1
 Ао a
Ао a


90 град В 1
Ü
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 507; Нарушение авторских прав?; Мы поможем в написании вашей работы!