Некоторые задачи оптимизации конструкций

§ 1. РАСЧЕТ ВАЛА МИНИМАЛЬНОЙ МАССЫ

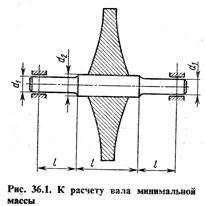
Рассмотрим ступенчатый быстро вращающийся вал с тяжелым диском посредине (рис. 36.1).

Если масса диска существенно больше ожидаемой массы вала (р — массовая плотность материала вала)

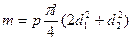
то поперечные размеры вала (диаметры d₁ и d₂) будут оп­ределяться не условиями прочности, а условиями динами­ческой устойчивости (см. гл. 14).

Во избежание больших поперечных колебаний вала его рабочая угловая скорость

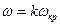
(36.1)

где ω_кр — критическая угловая скорость; к — коэффициент, к < 0,7.

Критическая угловая скорость вала

■ (36.2)

здесь α — податливость вала (прогиб среднего сечения вала от действия единичной силы);

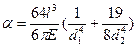(36.3)

где Е — модуль упругости материала вала.

Подставляя соотношения (36.2) и (36.3) в равенство (36.1), получим условие ди­намической устойчивости ва­ла в виде

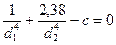
где

Определим диаметры ступеней вала d₁ и d₂ из условия минимума массы вала т.

Целевая функция в рассматриваемой задаче

а ограничение

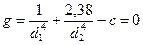
Записываем функцию Лагранжа

L = w + λg,

где λ — некоторая постоянная.

Необходимое условие экстремума этой функции

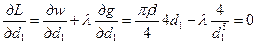
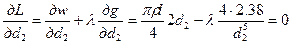
Из этих условий находим оптимальное соотношение диа­метров d₂/d₁ = 1,3. Подставляя это значение в последнее равенство, получим

§ 2. РАСЧЕТ МНОГОСТУПЕНЧАТОГО РЕДУКТОРА МИНИМАЛЬНЫХ РАЗМЕРОВ

При проектировании многоступенчатых редукторов возникает задача о распределении передаточных чисел между ступенями, которое бы обеспечило минимальные размеры и, как следствие, массу редуктора.

Показателем, определяющим габариты редуктора с цилин­дрическими колесами, является сумма межосевых расстояний между валами.

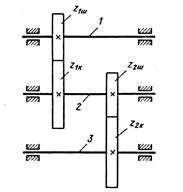
Рис. 36.2. Схема двухступенчатого ре­дуктора

Рассмотрим для простоты двух­ступенчатый редуктор (рис. 36.2). Межосевое расстояние для i-й сту­пени редуктора (i = 1, 2)

a _i = 0,5m _i (z_im + z_jK) = 0,5_jш (1 + i_j),

где m_i- модуль зубчатых колес i-й ступени; z_iш и z_iK - число зубь­ев шестерни и колеса; i — переда­точное отношение.

Сумма межосевых расстояний

a_∑ = а₁ + а₂= 0,5m₁ z_1ш (1 + i₁) + 0, 5 m₂ z_2ш (1 + i₂).

Если принять, что z_lш = z_{2 ш}, то это равенство можно записать в виде

a_∑ = 0,5m₁ z_1ш [1 + i₁ (1 + i₂)]. (36.4)

Модуль зуба определяется изгибной прочностью (см. с. 344). Используя равенство (см. с. 350), запишем (Y_F1 = Y_F2; K _Fβ1 = K _Fβ2 ^и K_m1 = К _m2)

где Т_1ш и T_2ш — вращающие моменты на шестернях первой и второй ступеней редуктора; ψ_bd1 и ψ_bd2— коэффициенты ширины колес первой и второй ступеней; [ σ_{F 1}] и [ σ_{F 2}] — допускаемые напряжения при изгибе для материалов шестерен первой и второй ступеней соответственно.

Учитывая, что T₂ = i₁T₁ при [ σ_{F 1}] = [ σ_{F 2}] и ψ_bd1 = ψ_bd2 получим

(36.6)

Подставляя равенство (36.6) в уравнение (36.4) находим

a_∑ = [1 + i₁ + 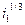(1 + i₂)].

Общее передаточное отношение

i = i₁i₂ (36.7)

Для нахождения экстремума функции a_∑ = w, в которой переменные i₁ и i₂ связаны зависимостью g=i — i₁i₂ = 0, также применим метод Лагранжа.

Функция Лагранжа

L= a_∑ + λg,

где λ— некоторая постоянная.

Условия экстремальных значений функции L запишем в виде

Решение дает следующую зависимость между передаточным отношением двух последовательных ступеней:

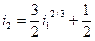
С учетом равенства (36.7) можно записать

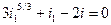(36.8)

Решение этого уравнения дано на рис. 36.3, а зависимость суммарного относительного межосевого расстояния от переда­точного отношения первой ступени редуктора показана на рис. 36.4. На этом рисунке виден ярко выраженный минимум относительного межосевого расстояния.

Из приведенного выше расчета несложно установить гра­ницы целесообразного (с точки зрения суммарного межосевого расстояния) перехода от одно- к двухступенчатому ре­дуктору.

Для одноступенчатого редуктора межосевое расстояние равно

а для двухступенчатого редуктора

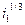a_∑ = [1 + i₁ + (1 +)].

Приравнивая а₁ = a_∑ получим условие, определяющее гра­ницу целесообразного перехода в виде

i (-1 ) + i₁ + 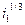=0. (36.9)

Это уравнение с учетом выражения (36.8) дает значение суммарного передаточного отношения i = 8,64, выше которого целесообразен переход с одно- на двухступенчатый редуктор независимо от числа зубьев шестерни.

Дата добавления: 2014-01-11