Базис линейного пространства. Его размерность

ЛИНЕЙНО НЕЗАВИСИМЫМИ НАБОРАМИ ВЕКТОРОВ

СВЯЗЬ МЕЖДУ ПОЛНЫМИ И

16°. Если e ₁, e ₂, …, e_m – линейно независимая, а f ₁, f ₂, …, f_n – полная системы векторов, то m £ n.

◀ Доказательство теоремы проведем от противного.

Допустим, что m > n (т.е. в полном наборе меньше векторов, чем в линейно независимом).

1) f ₁, f ₂, …, f_n – полная система. Тогда e ₁, f ₁, f ₂, …, f_n – полная и линейно зависимая, ибо e ₁ выражается через остальные e ₁ = b₁ f ₁ + b₂ f ₂ + … + b _nf _n.

При этом, по меньшей мере, одно из b _i ¹ 0, ибо в противном случае e ₁= q, что противоречит линейной независимости векторов. Не ограничивая общности можно считать, что b₁ ¹ 0, тогда f ₁ выражается через остальные векторы и его можно удалить из полной системы, не нарушая ее полноты.

Получена новая полная система векторов e ₁, f ₂, f ₃, …, f_n.

2) e ₁, f ₂, …, f_n – полная система. Тогда e ₁, e ₂, f ₂, …, f_n – полная и линейно зависимая, ибо e ₂ выражается через полную систему e ₂ = a₁ e ₁ + b₂ f ₂ + b₂ f ₂ + …+ + b _nf _n. При этом, по меньшей мере, одно из b _i ¹ 0, ибо в противном случае вектор e ₂ выразится через вектор e ₁, что противоречит линейной независимости системы e ₁, e ₂, …, e_m. Пусть b₂ ¹ 0, тогда f ₂ может быть выражено через остальные и его можно «прополоть».

Получится новая полная система векторов e ₁, e ₂, f ₃, f ₄, …, f_n.

3). Аналогично последовательно построим полные системы векторов

e ₁, e ₂, e ₃, f ₄, f ₅, …, f_n

e ₁, e ₂, e ₃, e ₄, f ₅, …, f_n

_{…………………………………}

e ₁, e ₂, e ₃, e ₄ , e ₅ , …, e_n.

4). Полнота системы e ₁, e ₂, e ₃, …, e_n противоречит линейной независимости более широкой системы e ₁, e ₂, …, e_{n ,} e_{n+ 1}, …, e_m. Полученное противоречие доказывает теорему. ▶

Система векторов e ₁, e ₂, …, e_n Î V называется базисом пространства V, если эта система векторов линейно независима и полна в V.

17°. Минимальный полный в V набор векторов является базисом.

◀ Докажем линейную независимость e ₁, e ₂, …, e_n.

Если они линейно зависимы, то, по крайней мере, один из векторов может быть записан как линейная комбинация остальных: e_n = a₁ e ₁ + a₂ e ₂ +…+ a _{n –1} e_{n –1}, следовательно, e ₁, e ₂, …, e_{n – 1,} полный набор, что противоречит минимальности исходного набора. ▶

18°. Максимальный линейно независимый в V набор является базисом.

◀ Докажем полноту набора e ₁, e ₂, …, e_n. Допустим, набор не полон. Тогда $ x Î V который не выражается как линейная комбинация e ₁, e ₂, …, e_n, тогда система x, e ₁, e ₂, …, e_n линейно независима, что противоречит максимальности исходного набора. ▶

19°. Всякое линейное пространство (кроме V º {q}) имеет базис.

◀ Доказательство можно провести построением: а) минимального полного набора или б) максимального линейно независимого набора. ▶

20°. Все базисы линейного пространства содержат одно и то же количество векторов.

◀ Пусть в пространстве V имеется два базиса 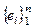и :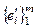

1) 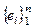– полный, а 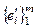– линейно независимый, тогда m ≤ n (т. 16°);

2) 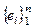– линейно независимый, а 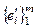– полный, тогда n ≤ m (т. 16°) Получаем m = n. ▶

Количество векторов в базисе называется размерностью пространства V и обозначается dim V.

21°. Чтобы линейно независимая система векторов была базисом необходимо и достаточно, чтобы количество векторов в этой системе равнялось размерности пространства

n = dim V. Доказать самостоятельно.

22°. Чтобы полная система векторов была базисом, необходимо и достаточно, чтобы количество векторов в этой системе равнялось размерности пространства n = dim V.

Доказать самостоятельно.

Дата добавления: 2014-01-11