Базис и размерность линейного подпространства

Ранее было определено понятие подпространства и установлено, что подпространство в свою очередь является пространством.

Для подпространства сохраняют смысл понятия полноты, линейной независимости,

базиса и размерности.

25°. Если E 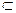V (подпространство), то dim E ≤ dim V.

◀ Линейно зависимый набор в E будет таковым и в V, поэтому максимальное количество линейно независимых векторов в E не превышает максимального количества линейно независимых векторов в V. ▶

26°. Если E 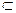V и dim E = dim V, то E ≡ V. Доказать самостоятельно.

Базис подпространства всегда можно дополнить до базиса пространства, но (как иллюстрирует картинка) из данного базиса пространства не всегда можно выделить базис подпространства.

27°. Линейная оболочка ℒ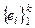является подпространством и dimℒ ≤ k.

Доказать самостоятельно.

28°. Линейная оболочка ℒ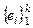– подпространство, натянутое на 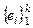– это наименьшее подпространство, содержащее эти векторы. Доказать самостоятельно.

Дата добавления: 2014-01-11