Поток поля. Дивергенция

Пусть векторное поле образовано вектором .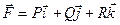

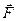Рис. 29

Для наглядности будем считать - вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность S находиться в этом потоке и пропускает жидкость. Требуется вычислить, какое количество жидкости протекает через поверхность S (рис. 29).

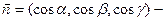единичный вектор нормали к рассматриваемой стороне поверхности S.

Потоком вектора 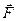через поверхность S называется интеграл П=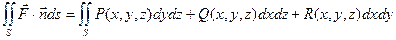- (этот интеграл ещё называют поверхностным интегралом II-го рода, 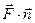- скалярное произведение)

Поток П вектора 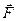есть скалярная величина, равная объему жидкости, которая протекает через поверхность S за единицу времени. В общем случае, поток поля вектора 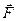пропорционален числу векторных линий, пронизывающих поверхность.

Т.О. если мы рассматриваем графическое изображение векторного поля, то можно судить о величине потока через одинаковые площадки по густоте векторных линий – там, где линии расположены ближе друг к другу, там больше и величина потока.

Рис. 30

Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объём V (рис. 30). Тогда поток вектора записывается в виде П =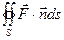. Если векторное поле 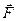- поле скоростей текущей жидкости, то величина потока П через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области V и втекающей в неё за единицу времени.

Если П>0, то из области V вытекает больше жидкости, чем в неё втекает. Это значит, что внутри области имеются дополнительные источники. Если П<0, то внутри области V имеются стоки, поглощающие жидкость.

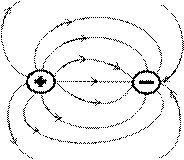Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии кончаются. Так в электростатическом поле источником является положительный заряд, стоком отрицательный заряд магнита (рис. 31).

Рис. 31

Если П=0, то из области V вытекает столько же жидкости, сколько в неё втекает в единицу времени; внутри области либо нет ни источников ни стоков, либо они таковы, что их действие взаимно компенсируется.

Дивергенция - численная характеристика плотности источника или стока поля в данной точке.

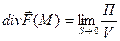- предел отношения потока поля через некоторую замкнутую поверхность к объёму, ограниченному этой поверхностью, когда поверхность S (рис. 30) стягивается в точку М, называется дивергенцией поля в точке М.

Если 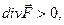то в точке М иметься источник поля плотности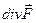

Если 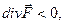то в точке М сток плотности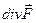

Если 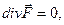то в точке М нет источников и нет стоков.

Дивергенция характеризирует мощность (интенсивность) источника или стока.

Формула для вычисления дивергенции:

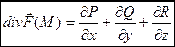
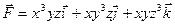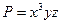
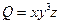
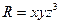
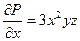
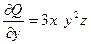
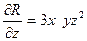
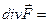
Пример: вычислить дивергенцию вектора в т. М(1;2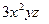;3)

+3+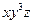

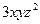
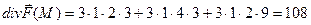> 0 - в точке находится источник.

Теорема: если функции P(x,y,z), Q(x,y,z), и R(x,y,z) - непрерывны вместе со своими частными производными первого порядка в ограниченной замкнутой области, имеющей объем V, то имеет место формула Остроградского-Гаусса.

П =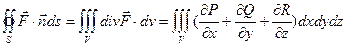

Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормаль, т.е. изнутри) равен тройному интегралу от дивергенции этого поля по объему V, ограниченному данной поверхностью.

Дата добавления: 2014-01-11