Виды относительных величин

Относительные величины структуры представляют собой соотношение частей я целого. Они характеризуют доли отдельных частей в целом. Рассчитываются по схеме: 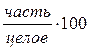. Выражаются обычно в процентах и в сумме равны 100%.

Пример. Численность населения города на 01.01.2007г. составила 148,4 млн. чел, в том числе мужчины - 69,8 млн. чел, женщины - 78,6 млн. чел. Определим относительные величины структуры:

мужчины - ;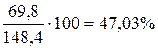

женщины - .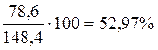

Относительные величины координации характеризуют соотношение отдельных частей целого с одной из них, взятой за базу сравнения. В выше приведенном примере возьмем за базу сравнения мужчин и определим относительную величину координации: 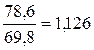, т.е. на каждую тысячу мужчин на 1.01.94г. в РФ приходилось 1126 женщин.

Относительные величины динамики характеризуют изменение явления во времени. Определяются путем деления величины показателя за данное время на величину этого же показателя за какое-либо аналогичное предшествующее время, взятое за базу сравнения. Выражаются относительные величины в процентах или коэффициентах.

Относительная величина планового задания выражает соотношение уровня планового задания на текущий период и фактического уровня данного показателя за предшествующий период.

Относительная величина выполнения плана - это соотношение фактического уровня показателя в текущем году и планового уровня на текущий год.

Пусть объем производства продукции в 2005 году составил 1186 млн. руб. Планом на 2006 год был предусмотрен выпуск продукции на 1250 млн. руб., а фактический выпуск за 2006 год составил 1200 млн. руб. Тогда:

а) относительная величина динамики будет равна:

,

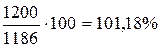б) относительная величина планового задания:

,

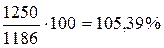в) относительная, величина выполнения плела:

.

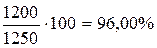При этом следует иметь в виду, что произведение относительных величин планового задания и выполнения плана равно относительной величине динамики.

.

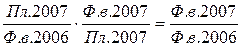Относительные величины интенсивности (уровня развития) выражают степень развития данного явления. Получаются в результате сопоставления двух разноименных абсолютных величин, связанных между собой. Например, производство различных видов продукции соотносится с численностью населения, в результате получаем производство той или иной продукции на душу населения. Относительные величины интенсивности имеют размерность тех величин, из соотношения которых получаются.

Относительные величины сравнения (наглядности) характеризуют сравнительные размеры одноименных величин, относящихся к одному и тому же периоду или моменту времени, но к разным объектам или территориям. Например, сравнение объема производства зерна за 2008 год в Вологодской и Ярославской областях, сравнение численности студентов на 1.01.2008г. в Вологодском государственном техническом университете и Вологодском государственном педагогическом университете и т.д. Относительные величины сравнения выражаются в коэффициентах или процентах.

ТЕМА: СРЕДНИЕ ВЕЛИЧИНЫ

1.Сущность и виды средних величин.

Средние в статистике - это показатели, выражающие типичные размеры признака для данной совокупности. В них взаимопогашаются индивидуальные отклонения, присущие отдельным единицам и показываются значения признака, характерные для всей совокупности.

Для определения средних величин используются следующие формулы:

1) Средняя арифметическая простая ;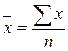

2) Средняя арифметическая взвешенная ;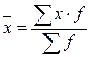

3) Средняя гармоническая взвешенная .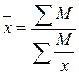

Чтобы правильно определить среднюю величину признака, необходимо, прежде всего, понять сущность этого показателя, уяснить соотношение каких величин он выражает, что является исходной базой для расчета среднего значения данного признака.

Допустим, нам следует определить средний размер заработной платы. Исходной базой для расчета средней заработной платы будет служить соотношение:

фонд заработной платы

число рабочих

Если фонд заработной платы обозначим М, число рабочих через f, а среднюю заработную плату через 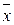, то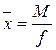

Выбор формулы для расчета средней величины зависит от имеющейся исходной информации.

Пример 1: Имеются следующие данные о заработной плате рабочих бригады

Табельный номер рабочего
Заработная плата, (д.е.)

Обозначив заработную плату через x, фонд заработной платы (М) определим как сумму заработной платы всех 10 рабочих, тогда

,

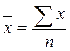где n – число значений x, равное числу рабочих бригады.

Следовательно, если каждое значение признака встречается один или одинаковое число раз, для расчета средней величины признака используется формула средней арифметической простой.

Пример 2: Имеются следующие данные:

№ бригады	Число рабочих	Заработная плата одного рабочего (д.е.)

Определить среднюю заработную плату рабочего по 2 бригадам.

Исходя из имеющихся данных фонд заработной платы по каждой бригаде определим путем умножения заработной платы одного рабочего (x) на число рабочих(f), а по двум бригадам вместе как сумму , тогда

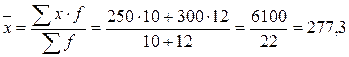д.е.

Если каждое значение признака встречается несколько раз, для расчета средней величины используется формула средней арифметической взвешенной.

№ бригады	Заработная плата одного рабочего, д.е.	Фонд заработной платы, д.е.

Пример 3: Имеются следующие данные

Помня, что исходной формулой для расчета средней заработной платы является 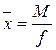, выражаем f как .

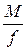Тогда 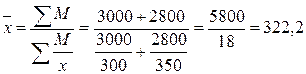д.е.

В данном случае расчет средней производим по формуле средней гармонической взвешенной.

2. Расчет средних по данным интервальных вариационных рядов.

Если варьирующий признак представлен в виде интервала «от-до», в качестве конкретных вариантов признака принимаются середины интервалов. Ширина открытого интервала принимается равной ширине примыкающего.

Среднее значение признака определяется по формуле средней арифметической взвешенной: .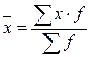

Расчеты обычно располагают в виде таблицы.

Пример 4: Имеются следующие данные о распределении рабочих по размеру заработной платы:

Заработная плата, (д.е.).	Число рабочих (f)	Середина интервала (x)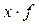
До 250 250 – 275 275 – 300 300 – 325 325 и более		237,5 262,5 287,5 312,5 337,5	2375,0 3937,5 5175,0 3750,0 1687,5
Итого

Серединное значение первого интервала равно 237,5;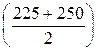

второго - 262,5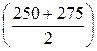и т. д.

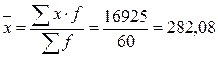д.е.

Свойства средней арифметической взвешенной.

1. Если все значения весов (f) увеличить или уменьшить в одно и то же число раз, то средняя не изменится.

2. Если все значения признака (x) увеличить (уменьшить) на одно и то же число A, то средняя увеличится (уменьшится) на это же число А.

3. Если все значения признака (х) увеличить (уменьшить) в одно и то же число K раз, то средняя увеличится (уменьшится) в K раз.

Изложенные свойства позволяют упростить расчет средней арифметической.

На основании указанных свойств, можно из всех значений признака вычесть постоянную величину А, разности сократить на общий множитель K, а все веса f разделить на одно и то же число и по измененным данным рассчитать среднюю 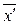. Затем если полученное значение средней 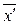, умножить на K, а к произведению прибавить А, то получим искомое значение средней арифметической по формуле:

,

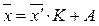где .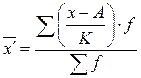

Средняя 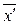, полученная из значений 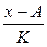, называется первым моментом, а вышеизложенный способ расчета средней - «способом моментов», или отсчетом от условного нуля.

Технику расчета средней арифметической «способом моментов» покажем на следующем примере:

Таблица 1

Заработная плата, д.е.	Число рабочих, f	x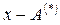
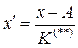
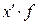
до 250 250 – 275 275 – 300 300 – 325 325 и более		237,5 262,5 287,5 312,5 337,5	- 2 - 25 +25 +50	- 2 - 1 +1 +2	- 20 -15 +12 +10
Итого					-13

(*) в качестве А обычно берут значение х, стоящее в середине вариационного ряда (А=287,5).

(**) K обычно равно ширине интервала (K=25)

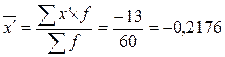
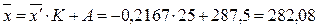д.е.

Как видим, результаты расчетов по исходной формуле средней арифметической взвешенной и по «способу моментов» совпадают.

3. Мода и медиана.

Мода в статистике - это значение признака, наиболее часто встречающее в изучаемой совокупности.

Медиана - это значение признака у единицы совокупности, делящей ранжированный ряд пополам (или стоящей в середине ранжированного ряда).

В дискретном ряду распределения модой является вариант признака, имеющий наибольшую частоту.

Пример: Распределение рабочих по тарифному разряду:

Разряд						Итого
Число рабочих

Наибольшее число рабочих (18) имеют третий разряд. Следовательно, мода для данной совокупности – 3 разряд.

Для нахождения медианы строится ряд накопленных частот.

Разряд	Число рабочих	Накопленная частота
		5+8=13 13+18=31 31+16=47 47+11=58 58+9=67
Итого

В данной совокупности состоящей из 67 единиц, в середине ранжированного ряда будет находиться 34-й рабочий 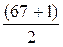. Рабочих с 1, 2, 3 разрядом насчитывается 31. Эта величина меньше порядкового номера медианы. Накопленная частота для 4 разряда - 47, т. е. превышает порядковый номер медианы. Отсюда следует, что рабочий, имеющий порядковый номер 34 принадлежит к 4-й тарифной группе. Следовательно, медиана в нашем примере - четвертый разряд.

В интервальных рядах распределения мода рассчитывается по следующей формуле:

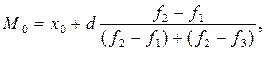где 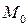- мода;

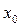- нижняя граница модального интервала (имеющего наибольшую частоту);

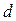- ширина модального интервала;

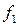- частота интервала, предшествующего модальному;

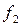- частота модального интервала;

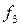- частота интервала, следующего за модальным.

Для нахождения медианы в интервальном ряду используют формулу:

,

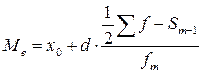
где 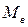- медиана;

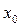- нижняя граница медианного интервала (накопленная частота которого содержит единицу, стоящую в середине ряда);

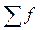- сумма частот ряда (численность совокупностей);

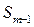- накопленная частота предмедианного интервала (предшествующего медианному);

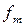- частота медианного интервала.

Пример: Имеются следующие данные с дневной выработкой рабочих:

Дневная выработка (тыс. руб.)	Число рабочих	Накопленная частота
40-50 50-60 60-70 70-80 80-90		158 (70+88) 255 (158+97) 362 (255+107) 441 (362+79)
Итого

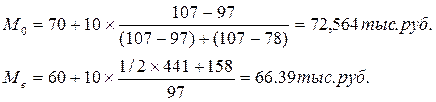
ТЕМА: ПОКАЗАТЕЛИ ВАРИАЦИИ

Дата добавления: 2014-01-11