Виды дисперсий и правило их сложения

Всякая совокупность, состоящая из значительного числа единиц, может быть расчленена по тому или иному признаку на части, которые называют частными совокупностям или группами.

Совокупность, состоящую из нескольких групп, называют общей.

Для общей и частной совокупностей могут быть определены средние величины и дисперсии, которые соответственно называются общими и групповыми.

,

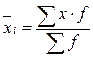
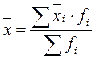где 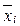- групповая средняя;

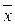- общая средняя;

х - индивидуальные значения признака;

f - число единиц, обладающих данным значением признака;

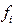- численность единиц в группе.

Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней .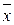

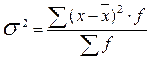
Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней).

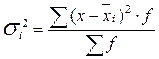
Групповая дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы.

Средняя из групповых (частных) дисперсий - это средняя взвешенная из групповых дисперсий (или остаточная):

.

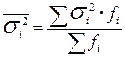Средняя из групповых дисперсий не равна общей дисперсии, т.к. она не учитывает колеблемости признака между группами.

Поскольку групповые средние (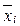) являются варьирующей величиной, то может быть определена их дисперсия.

Межгрупповая дисперсия характеризует вариацию результативного признака за счет группировочного признака. Она равна среднему квадрату отклонений групповых средних (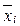) от общей средней ()

.

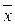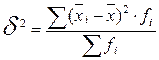Между общей, средней из групповых и межгрупповой дисперсиями существует следующая зависимость:

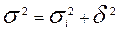, т. е. общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это соотношение называют правилом сложения дисперсий.

Достоверность правила сложения дисперсий покажем на примере.

Имеются следующие данные о выполнении норм выработки рабочими участка:

Группы рабочих	Выполнение норм выработки, %
до	90-100	100-110	110-120	120-130	130-140	140-150	и выше	Итого
Окончившие ПТУ Не прошедшие обучение	-						-	-
Итого

Для расчета средних величин и дисперсий используем способ «моментов»(см. табл.3).

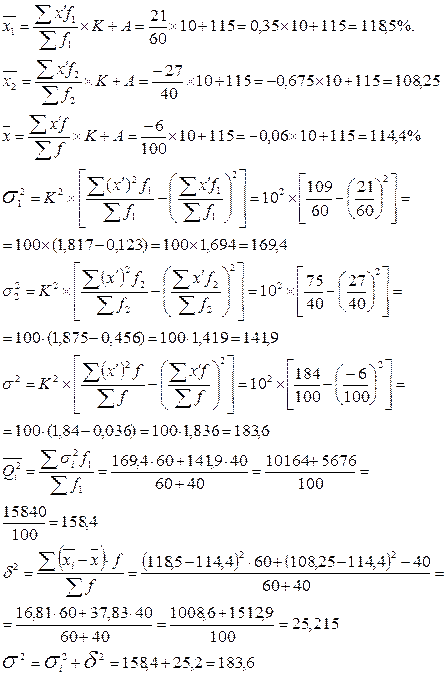
Таблица 3

Расчетная таблица

Выполнение норм выработки, %

Серединное значение, ()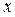

Число рабочих

х-А А =115

x-A K K=10 (х’)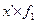

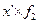
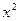
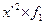
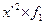
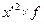
Окончивших ПТУ

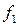
Не прошедших обучение

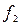
всего

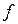
до 90 90-100 100-110 110-120 120-130 130-140 140-150 150 и более

-

- -

-30 -20 -10 +10 +20 +30 +40

-3 -2 -1 +1 +2 +3 +4

-4 -14 +11 +12 +12 +4

-9 -10 -16 +4 +4

-9 -14 -30 +15 +16 +12 +4

Итого

-27

-6

Тема: ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Дата добавления: 2014-01-11