Обработка результатов измерений

Подготовка к работе и проведение эксперимента

Задание

1. Провести градуировку термопары и поверку цифрового термометра с помощью платинового терморезистора. Количество стационарных режимов, а также число измерений в каждом режиме согласовать с преподавателем.

2. Рассчитать значения сопротивление резистора, R _T, и температуру T (R _T), пользуясь градуировочным уравнением для образцового термометра сопротивления в стационарных состояниях.

3. Построить функцию преобразования E (T) и градуировочную зависимость T (E).

4. Определить поправку D Е для стандартной термопары, используя сравнение результатов градуировки термопары с табулированными данными Т _станд для стандартной термопары по соотношению

D_станд =T - Т _станд ,

где Т - температура, измеренная термометром сопротивления в стационарном режиме, Т _станд. - соответствующее табулированное значение температуры для стандартной термопары.

5. Провести оценку погрешности, D, температуры, которая измерена с помощью термопары 8, используя полученные результаты градуировки термопары. Оценить случайную составляющую D_случ погрешности температуры, измеренной с помощью термопары.

Включить термостат и вывести его на заданный режим. Для этого с помощью контактного термометра термостата установить заданное значение температуры и включить нагреватель термостата. При достижении стационарного температурного режима провести измерения температуры. Результаты измерений занести в протокол.

Протокол наблюдений

№	t, ч, мин	U Т, мВ	U к, мВ	Е, мВ	Т стекл, ^ОС	Т цифр, ^ОС

С помощью данных, включенных в протокол, следует выполнить следующие действия.

1. Вычислить сопротивление R _T платинового термометра, используя (2.5).

2. Вычислить температуру, измеренную термометром сопротивления. Эта температура определяется градуировочным уравнением в форме

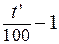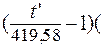
T = t +0,015[)][], (2.7)

где t’ - вспомогательный параметр, называемый как «платиновая» температура, ^о С.

Величина t’ находится из решения уравнения в виде

t’ = 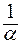(w- 1) + 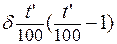, (2.8)

где w = R(T)/R₀, R(T) - сопротивление термометра при измеряемой температуре; R₀ = 10,0923 Ом - сопротивление термометра притемпературе 0 ^О С; a = 3,9141·10^-3, d=1,49187 - эмпирические коэффициенты уравнения, характеризующие данный термометр сопротивления; 100, 419,58, 630,74 - температуры (^оС): 1) кипения воды, 2) затвердевания цинка и 3) затвердевания сурьмы; эти значения получены при давлении равном одной физической атмосфере.

3. Методом наименьших квадратов получить: 1) функцию преобразования E (T) и 2) градуировочную зависимость T (E), используя (2.3, 2.4). Сравнить T (E) и соответствующие стандартные табличные величины T [1].

4. Оценить случайную погрешность измерения сопротивления терморезистора.

5. Оценить случайную погрешность измерения термоЭДС.

6. Оценить приборную погрешность температуры, измеренной платиновым терморезистором.

7. Оценить приборную погрешность измерения термоЭДС.

8. Построить графики T (E), E (T), E _станд(T) и D_станд(T), а также графики локальных отклонений D T _i(T) и D E _i(T), используя соотношения

D T_i = T_i -T _средн, D E_i = Е_i -Е _средн . (2.9)

Дата добавления: 2014-01-11