Шестнадцатеричную

ПЕРЕВОД ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ В ДВОИЧНУЮ, ВОСЬМЕРИЧНУЮ И

Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере чисел из десятичной системы в двоичную, при этом необходимо учитывать, что алгоритмы перевода целых и правильных дробей будут различаться.

Алгоритм перевода целых десятичных чисел в двоичную систему счисления.

Пусть А_цд – целое десятичное число, разложим его в ряд по основанию 2. Тогда в его записи в развернутой форме отсутствуют отрицательные степени основания, т.е. числа 2:

.

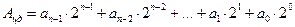На первом шаге разделим число А_цд на основание двоичной системы, т.е. на 2. Частное от деления будет равно:

,

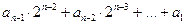а остаток равен .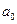

На втором шаге целое частное опять разделим на 2, остаток от деления будет .

Если продолжать этот процесс деления, то после n -го шага получим последовательность остатков:

.

Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме: .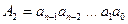

Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число.

Алгоритм перевода целого десятичного числа в двоичное будет следующим:

1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получим частное меньше делителя, т.е. меньше 2.
2. Получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.

В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:

Десятичное число/ целое частное	Делитель (основание системы)	Остаток	Цифры двоичного кода
			a0
			a1
			a2
			a3
			a4

В результате получаем двоичное число: .

Алгоритм перевода десятичных дробей в двоичную систему счисления.

Пусть А_дд – десятичная дробь, разложим ее в ряд по основанию 2. Тогда в его записи в развернутой форме отсутствуют положительные степени основания, т.е. числа 2:

На первом шаге умножим число А_дд на основание двоичной системы, т.е. на 2. Произведение будет равно:

Целая часть равна a _-1, именно это число и является значением первого дробного разряда двоичного числа.

На втором шаге оставшуюся дробную часть опять умножим на 2, получим целую часть, равную 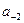, именно это число и является значением второго дробного разряда двоичного числа.

Описанный процесс необходимо продолжать до тех пор, пока в результате умножения не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.

Легко заметить, что последовательность полученных чисел совпадает с последовательностью цифр дробного двоичного числа, записанного в свернутой форме: .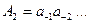

Алгоритм перевода десятичной дроби в двоичную будет следующим:

1. Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.
2. Получить искомую двоичную дробь, записав полученные целые части произведения в прямой последовательности.

В качестве примера, рассмотрим перевод десятичной дроби 0,75 в двоичную, записывая результаты в таблицу:

Десятичная дробь/ дробная часть произведения	Множитель (основание системы)	Целая часть произведения	Цифры двоичного кода
0,75			a-1
0,50			a-2
0,00

В результате получаем двоичную дробь: .

ТАБЛИЦА ПЕРЕВОДА ДЕСЯТИЧНЫХ ЧИСЕЛ В ДВОИЧНЫЕ ЧИСЛА

ДЕСЯТИЧНЫЕ	ДВОИЧНЫЕ

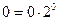
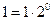
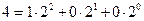
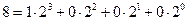
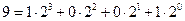
Дата добавления: 2014-01-11