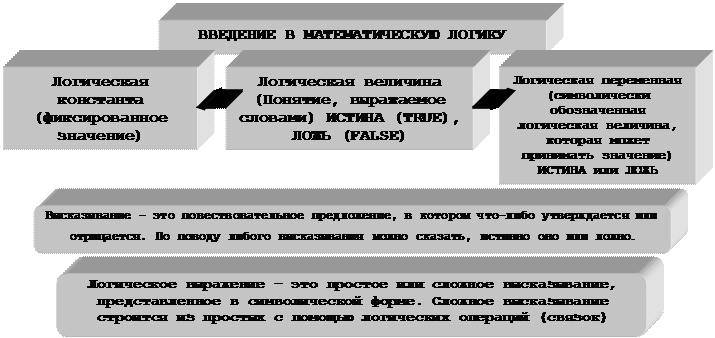
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно оно или ложно

ПОНЯТИЕ ОБ АЛГЕБРЕ ВЫСКАЗЫВАНИЙ.

Идею о возможности математизации логики высказал еще в XVII в. немецкий логик Готфрид Вильгельм Лейбниц. Он пытался создать универсальный язык, с помощью которого каждому понятию и суждению можно было бы дать числовую характеристику и установить такие правила оперирования с этими числами, которые позволили бы сразу определить, истинно данное суждение (высказывание) или ложно. Т.е. он предполагал, что споры между людьми можно будет разрешать посредством вычислений. Но идея Лейбница оказалась неподтвержденной, так как до сих пор не найден способ свести человеческое мышление к некоторому математическому исчислению.

Подлинный прогресс науки, называемой математической логикой, был достигнут в середине XIX в. прежде всего благодаря труду английского логика Джорджа Буля «Математический анализ логики». Он перенес на логику законы и правила алгебраических действий, ввел логические операции, предложил способ записи высказываний в символической форме. В трудах Дж. Буля и О. де Моргана математическая логика представлена как своеобразная алгебра – алгебра логики (алгебра высказываний).

Современная математизированная формальная логика представляет собой обширную научную область и находит широкое применение как внутри математики (исследование оснований математики), так и вне ее (анализ и синтез автоматических устройств, теоретическая кибернетика, в частности, искусственный интеллект).

Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Таким образом, объектами изучения алгебры высказываний являются высказывания.

Если высказывание A истинное, то будем писать «A = 1» и говорить «A – истинно». Если высказывание A ложное, то будем писать «A = 0» и говорить «A ложно».

В алгебре логики над высказываниями можно производить различные операции (подобно тому как в алгебре чисел определены операции сложения, деления, возведения в степень над действительными числами).

Дата добавления: 2014-01-11