Є зміна магнітного поля, яке пронизує

F

B dl

M

N

I

B B

q = + q

Fm Fm

u

u.

q = - q

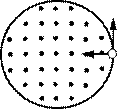
Рисунок 3.2

Визначивши напрям магнітної сили, а отже, і доцентрового прискорення, знайдемо напрям обертання частинки по колу (див. рис. 3.2, тут магнітне поле спрямоване до читача).

.

Якщо заряд q = + | q | є додатним, то напрями вектора B

та кутової швидкості w протилежні.

Коли заряд q = - | q |

є від’ємним, то ці напрями збігаються.

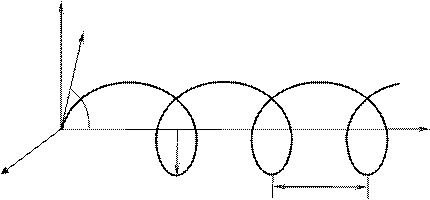
Таким чином, частинка в поперечній площині до магнітного поля рухається рівномірно по колу, а вздовж магнітного поля рухається зі сталою швидкістю. Результуючий рух є рухом частинки по спіралі, вісь якої паралельна магнітному полю (див. рис. 3.3).

Визначимо крок спіралі як відстань, яку частинка проходить вздовж осі Z за період

обертання T = 2p w (див. рис. 3.3):

h = T × u z

= 2p u

w 0 z

= 2p m u

qB 0

cos a. (3а.11)

õ

X

.

a Z

O

Y R

h

Рисунок 3.3

Таким чином, в однорідному магнітному полі заряджена частинка в загальному випадку рухається вздовж спіралі. Радіус та крок спіралі визначаються за формулами (3а.8) та (3а.11). Кутова частота обертання (кутова швидкість) подається співвідношенням (3а.9), період обертання – (3а.10).

Другий варіант

Розглянемо рух зарядженої частинки в однорідному магнітному полі, початкова швидкість якої спрямована під кутом a (див. рис. 3.1) до вектора індукції магнітного поля.

..

Для цього використаємо другий закон Ньютона

m d u dt = å Fi

та формулу для магнітної

...

складової сили Лоренца Fm = [u´ B ] і отримаємо

...

m d u = q [u´ B ]. (3б.1)

dt

У цьому співвідношенні

.

m, q – маса та заряд частинки, u – її швидкість, B

– індукція

...

магнітного поля. Спрямуємо вісь Z вздовж вектора B. Тоді

B = Bez. Запишемо рівняння

(3б.1) у проекціях на осі

X, Y, Z:

d u x

dt d u y

= q u B, m y

q

dt d u zdt

= -

m

= 0.

u x B,

(3б.2)

З останнього рівняння системи (3б.2) випливає, що u z

u z = u0 z = u0 cos a

є константою, тобто

Тут враховано, що початкова швидкість частинки спрямована під кутом a до осі Z (див.

рис. 3.1).

Якщо продиференціювати перше рівняння системи (3б.2) та в отриманий результат підставити друге рівняння системи (3б.2), то знайдемо

x

d 2u

= qB

æ ö

-ç ÷ u,

або

dt 2

è m ø x

d u x + w2u

= 0. (3б.3)

У рівнянні позначено

dt 2

w

x

= qB. (3б.4)

m

Цю величину називають циклотронною частотою. Рівняння (3б.3) в математиці називають

диференціальним рівнянням гармонічних коливань. Його розв’язок є

u x = A cos(w t + j0), (3б.5)

де A, j0

– сталі, які визначаються початковими умовами. Для того щоб впевнитись, що

(3б.5) є розв’язком (3б.3), достатньо підставити (3б.5) в (3б.3). Далі з першого рівняння (3б.2)

знаходимо

u = d u x

y dt

æ q

= - A sin(w t + j0ö

). (3б.6)

ç

è m

З’ясуємо сутність констант A та

B ÷

ø

j0. В початковий момент часу

t = 0

проекції

швидкості u x

і u y

мають значення

u0 x, u0 y. Підставляємо їх у (3б.5) та (3б.6) і отримуємо

2 2 2 2

u0 x = A cos j0, u0 y = - A sin j0. Звідси знаходимо, що

u0 x + u0 y = A

cos

j0+ sin

j0= A.

2 2

Зрозуміло, що

u0 x + u0 y

= u0^

– модуль складової початкової швидкості частинки,

яка перпендикулярна до осі Z. Таким чином,

.

A = u0^. Виберемо вісь X так, щоб в

початковий момент часу

знаходимо, що

t = 0

швидкість u0

лежала в площині XZ. Тоді з рис. 3.1

u0 x = u0sin a,

u0 y = 0.

Це означає, що

j0= 0,

u0^= u0sin a. З урахуванням вищесказаного, рівняння (3б.5)

та (3б.6) набирають вигляду

u x = u0^cos(w t),

u y = -u0^sin(w t),

(3б.7)

де u0^= u0 sin a.

Використаємо визначення швидкості і знайдемо залежність координат частинок від

часу:

dx x t

u x =

dt

= u0^cos(w t) Þ ò dx = ò u0^cos(w t) dt Þ

x 0 0

x = x 0+

u0^sin(w t), (3б.8)

w

dy y t

u y =

dt

= u0^sin(w t) Þ ò dy = ò - u0^sin(w t) dt Þ

y 0 0

y = y 0+

u0^(cos(w t) -1), (3б.9)

w

dz z t

u z = dt = u0 z Þ ò dt = ò u0 z dt Þ

z 0 0

z = z 0+ u0 z × t. (3б.10)

u

Початок координатних осей вибираємо так, щоб

x 0= 0, y 0-

0^= 0, z 0= 0. Це

w

приводить до спрощення математичних співвідношень без зміни фізичної сутності. Тоді з

(3б.8)-(3б.10) отримуємо

x = u0^sin(w t),

w

y = u0^cos(w t),

w

z = u0 z × t.

(3б.11)

Порівнюючи перші два рівняння (3б.11) з (3б.1) та (3б.2), робимо висновок, що частинка в площині XY рівномірно рухається по полу з радіусом

R = u0^

w

= u0 sina. (3б.12)

w

Кутова частота обертання частинки по цьому колу визначається циклотронною

частотою (3б.4) w = q B m.

Виходячи з третього рівняння системи (3б.11), стверджуємо, що частинка рухається вздовж осі Z рівномірно. Суперпозиція рівномірного руху вздовж осі Z та рівномірного руху по колу в площині XY дасть рух частинки по спіралі (див. рис. 3.3).

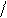Визначимо крок спіралі як відстань, яку частинка проходить вздовж осі Z за період обертання T = 2p w (див. рис. 3.3):

h = T × u z

= 2p u

w 0 z

= 2p m u

qB 0

cos a. (3б.13)

Таким чином в однорідному магнітному полі заряджена частинка в загальному випадку рухається по спіралі. Радіус та крок спіралі визначаються формулами (3б.12) та (3б.13). Кутова частота обертання (кутова швидкість) дається співвідношенням (3б.4), період обертання дорівнює

T = 2p = 2p × m. (3б.14)

w qB

§ 4 Закон Біо-Савара-Лапласа. Індукція магнітного поля, яке створене відрізком із струмом. Індукція нескінченно довгого прямого провідника зі струмом. Індукція на осі колового струму [5]

1 Біо й Савар провели в 1820 р. дослідження

магнітних полів, які створюються струмами, що проходять I

по тонких провідниках різної форми. Лаплас проаналізував dB

експериментальні дані, отримані Біо й Саваром, і встановив залежність, яка отримала назву закону Біо-Савара-Лапласа.

Відповідно до закону Біо-Савара-Лапласа індукція

магнітного поля, яка створюється елементом струму визначається за формулою

Idl, r

...

dB = m0

4p

I [ dl ´ r ]

, (4.1)

r 3

dl a

де dl

– вектор, модуль якого дорівнює елементарній

довжині ділянки зі струмом I і спрямований у той бік,

куди проходить струм (рис. 4.1); r – вектор, що проведено

.

.

Рисунок 4.1 – Індукція dB

від елемента струму в ту точку, у якій визначається

dB;

магнітного поля, що

r – модуль цього вектора; m0

що дорівнює

-7

– так звана магнітна стала,

-7

створюється елементом dl

провідника, по якому проходить струм I

m0 = 4p ×10

Тл∙м/А = 4p ×10

Гн/м, (4.2)

де Гн (генрі) – одиниця індуктивності (про цю одиницю детально мова буде йти далі).

Згідно з цим законом магнітне поле будь-якого струму може бути обчислене як векторна сума (суперпозиція) полів, які створюються окремими елементарними ділянками

струму Idl:

....

ò

B = ò

.

dB = m0

4p

I [ dl ´ r ].

r 3

Модуль вектора dB, виходячи з виразу (4.1), визначається співвідношенням

де a – кут між векторами dl

й r.

dB = m0

4p

I × dl × sin a, (4.3)

r 2

2 Застосуємо закон Біо-Савара-Лапласа для обчислення індукції магнітного поля, яке

створене відрізком із струмом, наприклад в точці O (див. рис. 4.2), яка знаходиться на відстані a від осі відрізка. При цьому вважаємо кути між напрямами векторів, проведених з кінців відрізка зі струмом до точки O і напрямом електричного струму I, відомими і

такими, що дорівнюють відповідно a1

й a2

(див. рис. 4.2).

dB O

d a a

r × da

a r

a M

P K a a1

I dl N

Рисунок 4.2 – До обчислення індукції магнітного поля, що ство- рюється відрізком провідника зі струмом

Розіб’ємо відрізок із струмом I на елементарні ділянки dl (див. рис. 4.2). Відповідно

.

до закону Біо-Савара-Лапласа елемент зі струмом Idl створює магнітне поле з індукцією

.

dB,

що визначається формулою (4.1). Зауважимо, що вектори

dB від усіх елементів струму I × dl

в точці O паралельні осі Z, яка перпендикулярна до площини рисунка (див. рис. 4.2). Тому

.

відповідно до принципу суперпозиції при визначенні індукції магнітного поля B

у точці O

можна перейти від геометричного до алгебраїчного підсумовування (інтегрування):

.

B = ò

l

.

..

dB = ez

× ò dB = e.

z

l

× m0× I

4p

sin a

×

r

ò 2

l

× dl, (4.4)

де dB – модуль вектора dB (див. формулу (4.3)); a – кут між векторами dl

й r.

Проаналізуємо вираз (4.4). Зрозуміло, що під знаком інтеграла у співвідношенні (4.4) кут a та довжина вектора r змінюються при переході від одного елемента довжини dl до іншого (див. рис. 4.2.). Тому перетворимо підінтегральний вираз так, щоб він залежав тільки від однієї змінної, наприклад кута a.

Неважко знайти зв’язок елемента dl з елементарним кутом d a

та довжиною вектора

r. З трикутника

D KMN

(див. рис. 4.2) випливає, що

dl × sin a = KM, а з трикутника

D OKN –

KM = r × d a. Звідси маємо

dl = r × d a sin a. Далі з трикутника

D OPN

можемо виразити

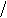довжину вектора r через відстань a та кут a:

вигляду

r = a / sin a. Тоді співвідношення (4.4) набуде

.. m 0 × I

a2 d a

a2

. m 0 × I

ò

B = ez × ×

a

4p r

= ez ×

4p × a

× òsin a × d a.

a1

Далі проведемо інтегрування і отримаємо шуканий вираз для індукції магнітного поля, що створюється відрізком провідника зі струмом:

B = m0× I

× (cos a1- cos a2). (4.5)

4p × a

3 Застосуємо закон Біо-Савара-Лапласа для обчислення індукції магнітного поля, яке створене нескінченно довгим прямим провідником зі струмом (див. рис. 4.3). Для цього використаємо формулу для індукції магнітного поля від відрізка із струмом (4.5).

O

.

B

a1

I a2 a

b

Рисунок 4.3 – До обчислення індукції магнітного поля, що ство- рюється нескінченним тонким провідником зі струмом

З рис. 4.3 випливає, що коли довжина відрізка b буде прямувати до нескінченності, то

кут

a1 буде прямувати до нуля, а кут

a2 – до

180°. Це означає, що коли відрізок

перетвориться в нескінченно довгий провідник із струмом (b = ¥), кути будуть мати значення

a1= 0, a2= 180°. (4.6)

Тоді індукцію від нескінченно довгого тонкого провідника із струмом знайдемо, підставивши значення (4.6) в (4.5):

B = m0 × I × (1- (-1)) = m0× I

, тобто

B = m0× I

. (4.7)

4p × a

2p × a

2p × a

Таким чином, отримали співвідношення

(4.7), яке визначає індукцію магнітного поля від X

O

нескінченного тонкого провідника із струмом I.

.

Слід зазначити, що напрям вектора B

можна

визначити за правилом правого гвинта: коли гвинт встановити паралельно струму й обертати його так, щоб поступальний рух гвинта був спрямований вздовж струму, то обертання шапочки гвинта буде визначати напрям силових ліній індукції магнітного поля.

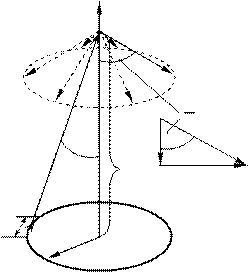
4 Застосуємо закон Біо-Савара-Лапласа для обчислення індукції магнітного поля на осі колового струму (див. рис. 4.4).

Розіб’ємо круговий виток, по якому

проходить струм I, на елементи довжини dl

(див. рис. 4.4). Елемент довжини dl зі струмом I

.

b

r

dl I

R

.

dB

x x

dB e. x

O ¢

p - b

2.

dB

.

dB ^

створює в точці O магнітне поле

dB, яке

Рисунок 4.4

.

визначається законом Біо-Савара-Лапласа (4.1). Відповідно до цього закону вектор dB є

перпендикулярним до радіуса-вектора. й вектора dl

відповідно до (4.3) дорівнює

(див. рис. 4.4), а його модуль

. m I × dl p m I × dl

| dB |= 0 × × sin = 0 ×. (4.8)

4p r 2

2 4p r 2

Тут враховано, що кут a між векторами r й dl

.

дорівнює

p / 2.

.

Подамо вектор dB

у вигляді суми двох векторів: вектора

.

Bxex, який спрямований

паралельно осі X, та вектора dB ^, який перпендикулярний до осі X (див. рис. 4.4).

.

Знайдемо векторну суму паралельних осі X компонент вектора

рисунка 4.4, неважко знайти проекцію

dB. Виходячи з

dB = - dB × cos(p / 2 - b) = - m0× I × dl × sinb. (4.9)

x 4p r 2

У цій формулі кут b – кут між віссю X та вектором r. Зазначимо, що для всіх елементів

струму Idl

кут b має одне і те саме значення (див. рис. 4.4)

sin b = R =

r

R

R 2+ x 2

. (4.10)

Відповідно до принципу суперпозиції знаходимо результуючу проекцію Bx

шляхом

підсумовування усіх елементарних проекцій

dBx

2p R

(або, в нашому випадку, їх інтегруванням)

Bx = ò dBx

= - m0× I

4p r 2

× sin b ×

m I

ò

dl = - 0 ×

r

4p 2

× sin b × 2p R =

= - m0×

4p

I ×

(R 2+ x 2)

R

R 2+ x 2

× 2p R = -

m0× I × R

2(R 2 + x 2)3/ 2

. (4.11)

Знайдемо векторну суму перпендикулярних до осі X компонент вектора

.

..

dB (dB ^).

Зазначимо – у цій сумі для кожного вектора

.

dB ^

можна знайти йому протилежний. Це

означає, що сума усіх векторів

dB ^

буде дорівнювати нулю.

.

Таким чином, результуюча індукція магнітного поля B

струмом буде визначатися співвідношенням

від колового витка зі

.

.

B = B e = -

m0× I × R.

x x 2(R 2 + x 2)3/ 2 ex. (4.12)

§ 5 Взаємодія двох нескінченно довгих паралельних провідників. Ампер –

одиниця вимірювання сили струму [15]

I

1 У 1820 р. Ампер експериментально встановив, що 1 2

два прямі паралельні струми притягуються, а

антипаралельні відштовхуються. Знайдемо силу взаємодії I 2

двох паралельних нескінченних струмів.

Розглянемо два нескінченно довгі паралельні провідники із струмами 1 і 2 (рис. 5.1). Індукція магнітного поля, що створюється нескінченно довгим провідником зі

F 21

F 12

A

струмом I 1

в точці A на відстані R від провідника 1,

R B 1

визначається співвідношенням

B = m0 I 1. (5.1)

1 2p R

Рисунок 5.1

Напрям вектора

.

B 1 можна визначити за правилом правого гвинта: коли гвинт

встановити паралельно струму й обертати його так, щоб поступальний рух гвинта був спрямований вздовж струму, то обертання шапочки гвинта буде визначати напрям силових

ліній індукції магнітного поля. У точці A відповідно до правила правого гвинта, вектор

.

індукції магнітного поля

B 1 спрямований «до нас» і перпендикулярний до провідника 2.

.

Тому кут a між провідником 2 і індукцією магнітного поля

B 1в точці A буде дорівнювати

p / 2. Тоді модуль сили Ампера, яка діє на відрізок довжиною l провідника 2 із струмом зможемо знайти із закону Ампера

I 2,

F 12

= B 1 I

l sin a = m0 I 1 I 2 l. (5.2)

2 2p R

Зрозуміло, якщо струми

I 1 і I 2

паралельні, то сила

F 12

за правилом лівої руки

спрямована до провідника 1. Аналогічно можна показати, що на провідник 1 із струмом I 1

діє сила

F 21

= m0 I 2 I 1 l,

2p R

..

але ця сила спрямована до провідника 2, тобто

F 12 = - F 21 (струми притягуються).

Якщо змінити напрям

..

I 1 (або

I 2), то зміняться напрями

.

F 12

.

і F 21. Оскільки

| F 12 |=| - F 21 |, то в загальному випадку сила взаємодії двох паралельних струмів буде

визначатися співвідношенням

F = m0 I 2 I 1 l. (5.3)

2p R

2 Вивчення взаємодії двох прямих сталих паралельних струмів дає змогу встановити одиницю струму – ампер як одну з основних у СІ. Ампер (А) – сила сталого струму, який, проходячи по двох паралельних прямолінійних провідниках нескінченної довжини малого кругового перерізу, розміщених на відстані 1 м один від одного у вакуумі, утворює силу взаємодії між ними, яка дорівнює 2 ×10-7 ньютон на кожний метр довжини.

З означення ампера і формули (5.3) знайдемо значення m0:

2 ×10-7Н= m0×1А ×1А ×1м, звідки m

2p ×1м 0

= 4p ×10-7 Н

А2

= 4p ×10-7 Гн

м

(генрі на метр).

§ 6 Сила, що діє на контур із струмом в однорідному магнітному полі. Момент сил, що діють на контур із струмом у магнітному полі. Вимірювання індукції магнітного поля за допомогою контуру зі струмом [5]

.

1 Знайдемо силу F, що діє на контур із струмом в однорідному магнітному полі

..

(B = const). Згідно із законом Ампера на елемент контуру dl

зі струмом I діє сила

..

dF = I [ dl ´ B ]. (6.1)

Результуючу усіх сил, що діють на усі елементи контуру, тобто силу, яка діє на контур, знайдемо шляхом інтегрування (6.1):

..

.

Винесемо сталі величини I й B

F = ò I [ dl ´ B ]. (6.2)

з під знака інтеграла. У результаті отримаємо

F = I [(ò dl)´ B ]. (6.3)

...

Інтеграл ò dl

береться за замкненим контуром і тому він дорівнює нулю. Тоді з (6.3)

.

випливає, що і сила дорівнює нулю

F = 0.

Таким чином, сила, що діє на контур зі струмом в однорідному магнітному полі, дорівнює нулю. Це справедливо для контурів будь-якої форми (у тому числі й неплоских) при довільному розміщенні контуру відносно напрямку поля. Істотною умовою для рівності нулю результуючої сили є лише однорідність поля.

У неоднорідному магнітному полі сила, що діє на контур із струмом, не дорівнює

нулю. Її визначають таким співвідношенням:

....

F = (pm × Ñ) B, (6.4)

....

m

де p. = I × S × n.

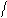
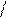
магнітний момент контуру зі струмом,

Ñ = ex ¶

¶ x + ey ¶

¶ y + ez ¶ ¶ z –

оператор набла.

2 Обчислимо результуючий обертальний

.

момент сил M, що діє на плоский контур із

струмом I в однорідному магнітному полі з

.

індукцією B.

На рис. 6.1 показано прямокутний контур,

.

x 1 X

dF 1

x 2

dF 2.

B.

орієнтований так, щоб вектор B

був

F 1.

F 2 a

паралельний двом з його сторонам. При pm

зазначених напрямках струму й поля (див.

рис. 6.1) на кожний елемент

dl 1

ділянки 1 – 2 діє

dl 1

dl 2

спрямована за площину рисунка сила Ампера

.

dF 1, модуль якої дорівнює

IBdl 1, а на кожний 1 b 4

елемент

dl 2

ділянки 3–4 діє спрямована «на нас»

.

Рисунок 6.1 – Плоский контур зі

сила Ампера

dF 2, модуль якої дорівнює

IBdl 2.

струмом в однорідному магнітному полі,

.

Ділянки 2–3 і 4–1 паралельні полю, тому сили на

них не діють.

індукція B

якого паралельна стороні b

.

Результуюча

.

F 1 сил

.

dF 1

прикладена до

контуру. Нормаль n і сила F 1

.

середини ділянки 1–2 і має модуль, що дорівнює

спрямовані «від нас», сила F 2

IBa. Аналогічно результуюча

.

F 2 сил

.

dF 2

спрямована «на нас»

..

прикладена до середини ділянки 3–4 і має модуль такої ж величини, що й

.

F 1. Момент сил F 1

й F 2

відносно довільної осі X (див. рис. 6.1) дорівнює

M = IBa × x 1+ IBa × x 2= IBa × (x 1 + x 2) = IBa × b = IBS.

Тут використано, що виходячи з геометричних міркувань

.

x 1+ x 2= b,

.

a × b = S, де S – площа

контуру. Врахувавши взаємну орієнтацію векторів M, B

струмом I, можна записати, що

і орту нормалі n контуру зі

...

Вираз

ISn

M = [(ISn) ´ B ]. (6.5)

є важливою характеристикою контуру площею S зі струмом I, який

називають магнітним моментом контуру

m

p. = ISn.. (6.6)

Вектор нормалі контуру n має одиничну довжину, спрямований перпендикулярно до площини контуру і пов’язаний з напрямом електричного струму, що проходить по контуру, правилом правого гвинта. Як випливає з (6.6), магнітний момент вимірюється в системі СІ

в A × м 2.

Тоді формулу (6.5) з урахуванням визначення магнітного моменту можна записати у

вигляді

.....

M = [ pm ´ B ],

(pm ^ B). (6.7)

.

Нагадаємо, що формула (6.7) отримана для випадку, коли вектор B

є паралельним площі

..

цього контуру (pm ^ B).

У випадку, коли вектори

.

p

.

.

m й B

паралельні (в цьому

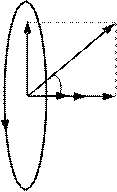B ^ B

випадку вектор B

є перпендикулярним до площі контуру), сили,

що діють на окремі елементи контуру, лежать в одній площині

(площині контуру) і, отже, не можуть створити обертальний

.

p

m

момент. Ці сили прагнуть розтягти (якщо. й B

p

m

B

однаковий напрям) або стиснути (якщо. й.

протилежні напрями) контур.

.

мають мають

a

p

..

n m B ||

p

m

Розглянемо випадок, коли вектори

. й B

утворюють I

.

довільний кут a (рис. 6.2). Розкладемо магнітну індукцію B на

дві складові:

.

B ||

.

– паралельну й B ^

– перпендикулярну до вектора

.

Рисунок 6.2 – Контур, нормаль n до площини

m

p., і розглянемо дію кожної складової окремо. Компонента

B ||

якого утворює з нап-

.

буде обумовлювати сили, що розтягують або стискають контур.

.

рямом вектора B

кут a

Компонента

B ^, що має модуль, який дорівнює

B sin a, приведе

до виникнення обертального моменту, який можна обчислити за формулою (6.7):

...

M = [ pm ´ B ^]. (6.8)

..

Оскільки [ pm ´ B ||] = 0, формулу (6.8) можна написати у вигляді

...

M = [ pm ´ B ]. (6.9)

Таким чином, отримали формулу (6.9), яка визначає результуючий обертальний момент сил, що діє на плоский контур із струмом I в однорідному магнітному полі з

.

індукцією B. Зазначимо, що ця формула є справедливою при будь-якій взаємній орієнтації

m

.

p

векторів

. і B. Можна довести, що вона є правильною для плоских контурів будь-якої

форми, що знаходяться в однорідному магнітному полі.

3 Формулу (6.9) можна застосовувати й для неоднорідних магнітних полів. Необхідно тільки, щоб розміри контуру були малі. Тоді впливом неоднорідності поля на обертальний

момент можна знехтувати. Такі контури й котушки можуть бути використані на практиці для

вимірювання індукції магнітного поля. У цьому випадку їх називають пробними.

Якщо пробний контур помістити в магнітне поле, то під дією обертального моменту

m

.

p

його магнітний момент

. встановиться уздовж індукції магнітного поля B

подібно, як це

відбувається з магнітною стрілкою. Таким чином, самовільна орієнтація контуру зі струмом

.

в магнітному полі дозволяє визначити напрям вектора індукції магнітного поля B.

Повернемо контур із цього положення на 90°. Обертальний момент у цьому випадку стане

максимальним. Вимірявши максимальний обертальний момент сил

M max

контуру зі

струмом, знаючи його магнітний момент, можемо знайти модуль індукції магнітного поля, використовуючи формулу (6.9):

B = M max/ pm. (6.10)

Таким чином, використовуючи контур зі струмом, можна виміряти як напрям, так і модуль вектора індукції магнітного поля.

§ 7 Робота при переміщенні контуру зі струмом у магнітному полі [9]

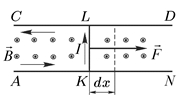
1 Розглянемо спочатку окремий випадок. Нехай паралельні провідники AN й CD

.

(рис. 7.1) розміщені в однорідному сталому магнітному полі з індукцією B, яке

перпендикулярне до площини рисунка й спрямоване «до нас». Ліворуч знаходиться джерело струму, яке не показано на рисунку. По проводах може вільно переміщуватися провідний

місток KL, що замикає струм I, який проходить по проводах, які розміщені ліворуч містка.

Якщо l – довжина містка, то на нього магнітне поле діє із силою Ампера переміщенні містка на відстань dx ця сила виконає роботу

dA = Fdx = IBldx = Id (BS),

F = IBl. При

де S – площа прямокутника AKLC. Величина BS є магнітним потоком через той самий

..

прямокутник. Позначивши його через

співвідношення

F = B × S = B × S, отримаємо для елементарної роботи

dA = Id F, (7.1)

а для скінченної роботи у випадку сталого електричного струму

A 12 = I (F2 - F1). (7.2)

Таким чином, робота, яка виконується магнітним полем над струмом, дорівнює збільшенню магнітного потоку, помноженому на силу струму I. При доведенні передбачалося, що струм I при переміщенні містка KL підтримувався постійним.

2 Формули (7.1) та (7.2) є правильними і в тому випадку, коли магнітне поле спрямовано довільно. Ці формули є

Рисунок 7.1

правильними також і для будь-якого витка зі струмом при довільному переміщенні його в сталому неоднорідному магнітному полі. Виток може не тільки переміщуватись як ціле,

але й довільно деформуватися. Для доведення достатньо подумки розбити виток на нескінченно малі елементи струму й розглянути нескінченно малі їх переміщення. При

нескінченно малому переміщенні елемента струму магнітне поле, у якому він переміщується, може вважатися однорідним. До такого переміщення можна застосувати вираз (7.1) для

елементарної роботи. Додаванням таких елементарних робіт для всіх елементів струму, на

які розбитий виток, знову отримуємо вираз (7.1), у якому d F

означає збільшення магнітного

потоку через весь виток. Після цього перехід від формули (7.1) до формули (7.2) відбувається простим інтегруванням. Підкреслимо ще раз, що при переміщенні витка сила струму у ньому повинна підтримуватися сталою. Це досягається шляхом відповідного збільшення електрорушійної сили джерела.

§ 8 Теорема Гаусса для магнітного поля у вакуумі. Теорема про циркуляцію вектора магнітної індукції [5]

.

1 Як відомо, елементарним потоком вектора A

величину

.

через площу dS

називають

..

d F = A × dS.

Виходячи із цього визначення, можемо записати елементарний потік вектора індукції

.

магнітного поля B

.

через площу dS

у вигляді

..

d F = B × dS. (8.1)

Магнітний потік через довільну площу S за визначенням дорівнює

..

F = ò B × dS. (8.2)

S

Однією з особливостей магнітного поля є те, що його силові лінії завжди замкнені,

.

тобто не мають ні початку, ні кінця. Внаслідок цього потік вектора B

замкнену поверхню дорівнює нулю (доводити це не будемо):

через будь-яку

..

ò BdS = 0. (8.3)

S

.

Ця формула виражає теорему Гаусса для вектора індукції магнітного поля B в

інтегральному вигляді: потік вектора магнітної індукції через будь-яку замкнену поверхню

дорівнює нулю.

Теорема Гаусса є математичним виразом того, що в природі відсутні «магнітні заряди» – джерела магнітного поля, на яких би починалися або закінчувалися лінії магнітної

індукції.

Зазначимо, що магнітний потік Ф вимірюється у веберах (1 Вб=1 Тл·1 м2).

2 Для того щоб отримати теорему Гаусса в диференціальному вигляді, використаємо теорему Остроградського-Гаусса

...

ò A × dS = ò divA × dV, (8.4)

S V

де об'єм інтегрування V знаходиться в середині замкненої поверхні інтегрування S.

Виходячи з теореми Остроградського-Гаусса й (8.3), отримаємо для індукції магнітного поля

...

ò BdS = ò divBdV = 0,

S V

або

.

divB = 0. (8.5)

.

Співвідношення (8.5) виражає теорему Гаусса для вектора індукції магнітного поля B в

диференціальному вигляді.

..

3 Тепер знайдемо циркуляцію вектора B. Нагадаємо, що циркуляцією вектора B за

визначенням називають інтеграл по замкненому контуру G:

.

де dl

ò B × dl, (8.6)

G

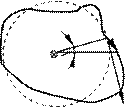– елемент замкненого контуру G, по якому виконують інтегрування. Обчислимо циркуляцію

.

вектора B

для випадку поля

G 2 - d a

нескінченного прямого струму. Нехай

замкнений контур G лежить у I I

площині, яка перпендикулярна до d a

провідника, по якому проходить

такий електричний струм (рис. 8.1). У B

+ d a

G

.

кожній точці контуру вектор B

спрямований за дотичною до кола, що проходить через цю точку. Через

центр цього кола проходить

а) б)

Рисунок 8.1 – До обчислення циркуляції для поля прямого струму. Струм перпендикулярний до площини рисунка і спрямований за рисунок

.

електричний струм I і спрямований за площу рисунка. Подамо B × dl

.

у вигляді B × dlB

(dlB –

проекція dl

на напрям вектора B). З рисунка випливає, що

dlB

дорівнює

bd a, де b –

відстань від провідника зі струмом до

dl; d a

– кут, на який повертається радіальна пряма

при переміщенні уздовж контуру на відрізок dl. Підставимо в (8.6) це значення для індукції B нескінченно довгого провідника зі струмом й отримаємо

dlB, вираз

..

Bdl =

Bdl =

m02 Ibd a = m0 I d.

ò ò B

G G

ò4p b

2p ò a

При обході контуру G, що охоплює струм (рис. 8.1 а), радіальна пряма увесь час

повертається в одному напрямку, тому

ò d a = 2p. Якщо струм не охоплюється контуром G

(рис. 8.1 б), то радіальна пряма повертається спочатку в одному напрямку (ділянка 1–2), а

потім у протилежному (ділянка 2–1). Кути

d a, що відповідають поворотам у протилежні

боки, відрізняються знаком. Тому ò d a = 0. Обидва результати можна виразити формулою

.

ò Bdl

G

= m0 I, (8.7)

де I – струм, який охоплюється контуром G. Якщо контур G струму не охоплює, отже, циркуляція також дорівнює нулю.

I = 0 і,

Знак циркуляції залежить від напрямку обходу контуру. Якщо цей напрям утворює з напрямом струму правогвинтову систему, то, як випливає з рис. 8.1 а, вираз (8.7) додатний, у протилежному разі – від’ємний. Знак можна врахувати, вважаючи I алгебраїчною величиною, причому додатним потрібно вважати струм, напрям якого утворює із напрямом обходу контуру правогвинтову систему; струм протилежного напрямку буде від’ємним.

Ми отримали формулу (8.7) для прямого струму й плоского контуру. Однак можна

довести, що ця формула є правильною й для неплоского контуру, і для струму, що проходить по провіднику довільної форми.

За допомогою принципу суперпозиції отриманий результат легко узагальнюється на випадок декількох струмів:

.

ò Bdl

= m0å Ik

(8.8)

G k

Формула (8.8) виражає теорему про циркуляцію вектора індукції магнітного поля у

.

вакуумі: циркуляція вектора B

по довільному контуру G дорівнює алгебраїчній сумі

струмів, що охоплюються контуром G, яка помножена на m0.

Зазначимо, що формула (8.8) справедлива тільки для поля у вакуумі й за умовою відсутності змінних у часі електричних полів. Поле, циркуляція якого не дорівнює нулю, називається вихровим. Таким чином, магнітне поле є вихровим.

§ 9 Магнітне поле тороїда. Магнітне поле нескінченного соленоїда [5]

1 У вченні про магнітне поле сталих струмів теорема про циркуляцію магнітного поля

.

ò Bdl

= m0å Ik, (9.1)

де å Ik

G k

дорівнює алгебраїчній сумі струмів, що охоплюються контуром G, відіграє

приблизно таку саму роль, що і теорема Гаусса в електростатиці. За умови наявності симетрії

у розподілі електричних струмів теорема про циркуляцію дозволяє достатньо просто визначити індукцію магнітного поля.

2 Тороїдом називається провідник, який навитий на каркас, що має форму тора

(рис. 9.1). Застосуємо теорему про циркуляцію магнітного поля (9.1) для знаходження магнітного поля, яке створює електричний струм I, що проходить по тороїду. Візьмемо контур інтегрування G у вигляді кола радіуса r, центр якого збігається із центром тороїда

.

(див. рис. 9.1). У наслідок симетрії розподілу електричних струмів вектор B

у кожній точці

.

контуру G спрямований вздовж дотичної до нього. Отже, циркуляція вектора B

цього контуру дорівнює

вздовж

.

ò Bdl

G

.

= B × 2p r,

де B

– магнітна індукція у тих точках, де проходить контур G.

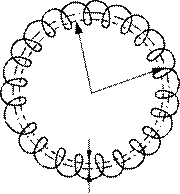Якщо контур проходить усередині тороїда, він

охоплює струм

å Ik = 2p RnI, де R – радіус тороїда; n –

число витків на одиницю його довжини. Тоді згідно з r

теоремою про циркуляцію магнітного поля (9.1) можемо

записати R

B × 2p r = m0× 2p RnI,

звідки знаходимо індукцію магнітного поля всередині тороїда h

B = R m

r 0

nI. (9.2а)

Коли контур проходить за межами тороїда, то він струмів не

Рисунок 9.1 – Тороїд ра-

охоплює. Тому в цьому випадку

тороїда поле дорівнює нулю

B × 2p r = 0. Отже, за межами

діуса R. Штриховою ліні-

єю радіуса r показано кон- тур інтегрування G

B = 0. (9.2б)

Таким чином, поле зосереджене усередині тороїда. Зазначимо, що поле тороїда не є однорідним, у точках з різним значенням r індукція магнітного поля, як це в

Дата добавления: 2014-01-11