Непрерывность функций

◙ Функция у = f (x), определенная при x = х ₀ и всех значениях х, достаточно близких к х ₀ , называется непрерывной при x = х ₀ (в точке х ₀ ), если

f (х ₀ + 0) = f (х ₀ – 0) = f (х ₀).

Это по определению предела означает, что для каждого положительного числа ε, как бы мало оно не было, можно указать такое d (e) > 0, что для всех х, отличных от х ₀ и удовлетворяющих неравенству | х – х ₀ | < d (e), имеет место неравенство ½ f (x) – f (х ₀) ½< e.

Введем понятия приращений:

приращение аргумента: ∆x = x – х ₀,

приращение функции: ∆ у = f (x) – f (х ₀).

Тогда описательно геометрически непрерывность функции в точке x = х ₀ означает, что бесконечно малому приращению аргумента (от начального значения x = х ₀) соответствует бесконечно малое приращение функции.

Опираясь на свойства пределов, можно получить

Основные свойства непрерывных в точке функций:

1) Если функции f ₁(x) и f ₂(x) непрерывны в точке x = х ₀ , то сумма

(f ₁(x) + f ₂(x)) также есть непрерывная функция в точке x = х ₀.

(Это свойство справедливо для любого конечного числа слагаемых.)

2) Если функции f ₁(x) и f ₂(x) непрерывны в точке x = х ₀, то

произведение (f ₁(x)∙ f ₂(x)) также есть непрерывная функция в точке x = х ₀.

(Это свойство справедливо для любого конечного числа множителей.)

3) Если функции f ₁(x) и f ₂(x) непрерывны в точке x = х ₀, то

частное также есть непрерывная функция в точке x = х ₀ ,

за исключением тех значений независимой переменной, при которых знаменатель обращается в нуль.

4) Если функция u = φ (x) непрерывна в точке x = х ₀ и f (u) непрерывна в точке u ₀ = φ (х ₀), то сложная функция f [ φ (x)] непрерывна в точке x = х ₀.

5) Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

непрерывные на отрезке функции

Пусть a £ x £ b.

◙ Функция непрерывна на отрезке [ a, b ], если функция непрерывна при любом значении х из этого промежутка.

При этом , .

Основные свойства непрерывных на отрезке функций:

1) Если f (x) непрерывна на отрезке [ a, b ], то существует в этом промежутке, по крайней мере, одно такое значение х, при котором f (x) принимает свое

наибольшее значение и, по крайней мере, одно такое значение х, при котором f (x) принимает свое наименьшее значение.

2) Если f (x) непрерывна на отрезке [ a, b ], причем f (а) = т, f (b) = п,

то для любого k, заключенного между числами m и n, найдется такая точка x = с, что f (с) = k.

В частности, если f (a) и f (b) разных знаков, то найдется такая точка x = с, что f (с) = 0.

Односторонняя непрерывность.

Точки разрыва и их классификация

◙ Если в какой-то точке x = х ₀ для функции у = f (x) не выполняется, по крайней мере, одно из условий непрерывности, то при x = х ₀ функция у = f (x) разрывна. Точка x = х ₀ в этом случае называется точкой разрыва функции.

Если пределы f (х ₀ – 0) и f (х ₀ + 0) существуют, то разность

f (х ₀ + 0) – f (х ₀ – 0) называется разрывом, или скачком, функции f (x) при

x = х ₀ (в точке х ₀).

При этом функция f (x) имеет в точке х ₀ разрыв первого рода, если пределы справа и слева конечны, но не равны друг другу, т.е.

f (х ₀ + 0) ¹ f (х ₀ – 0).

Если f (х ₀ + 0) = f (х ₀ – 0) ¹ f (х ₀), то х ₀ – устранимая точка разрыва первого рода.

Функция f (x) имеет в точке х ₀ разрыв второго рода, если хотя бы один из пределов f (х ₀ – 0) (или f (х ₀ + 0)) бесконечен или не существует.

Пример. Исследовать функции на непрерывность. Определить характер точек разрыва: 1) ; 2).

Решение.

1) , .

Так как 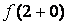, то х ₀ = 2 точка разрыва первого рода,

–= 1 – скачок функции в этой точке.

2) ,

.

Так как один из односторонних пределов , то х ₀ = 5 точка разрыва второго рода.

Дата добавления: 2014-01-11