КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства соленоидального поля. Соленоидальное поле и его свойства
|
|
|
|
Соленоидальное поле и его свойства.
Свойства дивергенции.
1) Линейность. 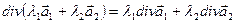
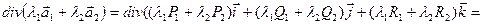

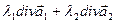 .
.
2)  , где
, где  - постоянное векторное поле.
- постоянное векторное поле.

3) 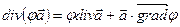 , где
, где 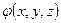 - скалярное поле.
- скалярное поле.
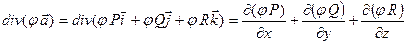 =
= 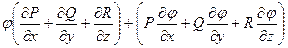 =
= 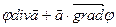 .
.
Векторное поле 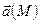 называется соленоидальным в области V, если в любой точке M этой области
называется соленоидальным в области V, если в любой точке M этой области 
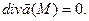
1) Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.
Необходимость следует из формулы Остроградского – Гаусса, достаточность – из инвариантного определения дивергенции.
2) Поток соленоидального поля через любую поверхность, окружающую изолированный источник или сток, один и тот же.

    
| Рассмотрим две замкнутых поверхности  и и  , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям.
Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости.
В той и другой области поле соленоидально. Следовательно, , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям.
Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости.
В той и другой области поле соленоидально. Следовательно,
|
поток векторного поля через границы этих областей равен нулю.
 ,
,
 .
.
Складывая эти выражения, получим  .
.
3) Поток соленоидального поля через произвольное сечение векторной трубки один и тот же.
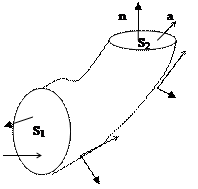
| Обозначим Sбок –боковую поверхность векторной трубки. На боковой поверхности направления нормали и векторного поля ортогональны, так как векторная трубка образована векторными линиями, а вектор поля направлен по касательной к векторной линии. Поэтому поток векторного поля через боковую поверхность векторной трубки равен нулю (ПSбок.= 0).
Учитывая направления нормалей и вектора поля на сечениях векторной трубки S1 и S2, а также соленодальность поля, получим
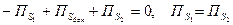 . .
|
Следствие. Векторные линии соленоидального поля не могут начинаться и заканчиваться внутри поля.
В самом деле, иначе конечный поток приходился бы на нулевую площадь источника или стока, что требовало бы бесконечной мощности источника или стока.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1119; Нарушение авторских прав?; Мы поможем в написании вашей работы!