Второй признак сравнения

Пусть . Тогда ряды 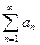и сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится.

Доказательство. Раскроем определение предела. .

.

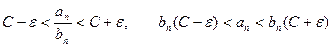Если ряд 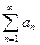сходится, то по 1 признаку сравнения ряд сходится (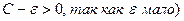, ряд сходится (свойство сходящихся рядов).

Если ряд сходится, то ряд сходится (свойство сходящихся рядов), тогда по 1 признаку сравнения ряд 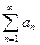сходится.

Пусть ряд 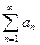расходится. Если ряд сходится, то по предыдущему ряд 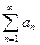сходится (противоречие).

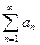Пусть ряд расходится. Если ряд сходится, то по предыдущему ряд сходится (противоречие).

Пример. Ряд с расходится по второму признаку сравнения (ряд сравнения – гармонический ряд).

Ряд 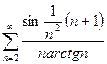сходится. - ограничена. Ряд сравнения - сходящийся ряд Дирихле.

Дата добавления: 2014-01-11