
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предельная форма радикального признака Коши
|
|
|
|
Пусть 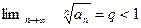 , тогда ряд
, тогда ряд 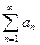 сходится.
сходится.
Пусть 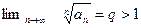 , тогда ряд
, тогда ряд 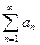 расходится.
расходится.
Доказательство. Пусть 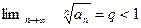 , тогда
, тогда 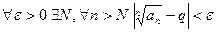 .
.
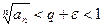 при малом
при малом  . Ряд
. Ряд 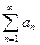 сходится по конечной форме радикального признака Коши.
сходится по конечной форме радикального признака Коши.
Пусть 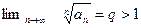 , тогда
, тогда 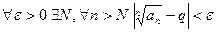 .
. 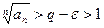 при малом
при малом  . Тогда
. Тогда 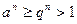 , ряд
, ряд 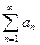 расходится, так как необходимый признак сходимости ряда не выполнен.
расходится, так как необходимый признак сходимости ряда не выполнен.
Пример. 
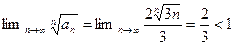 , ряд сходится по радикальному признаку Коши в предельной форме.
, ряд сходится по радикальному признаку Коши в предельной форме.
Замечание. У каждого признака сходимости есть своя «зона нечувствительности». Ни признак Даламбера, ни радикальный признак Коши не позволяют установить расходимость гармонического ряда. Проверьте это. Гармонический ряд расходится, но расходится так слабо, что попадает в «зону нечувствительности» указанных признаков. Интегральный признак Коши имеет меньшую «зону нечувствительности» и позволяет установить расходимость гармонического ряда.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 773; Нарушение авторских прав?; Мы поможем в написании вашей работы!