Лекция 13. Равномерно сходящиеся ряды

Функциональные ряды

Функциональный ряд – это ряд 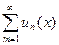, члены которого – функции 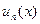, определенные в некоторой области V.

Определим частичную сумму ряда – тоже функцию .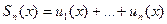

Зафиксировав некоторую точку x, мы имеем дело с обычным числовым рядом.

Функциональный ряд 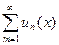называется сходящимся в точке x, если 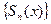сходится к или

, что .

Это - обычная или поточечная сходимость ряда, так как номер N зависит не только от , как в числовых рядах, но и от точки x. То есть в каждой точке x ряд сходится со своей скоростью.

Критерий Коши поточечной сходимости ряда. Это – критерий Коши для последовательности частичных сумм ряда.

Для того чтобы функциональный ряд 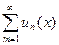сходился в точке x, необходимо и достаточно, чтобы .

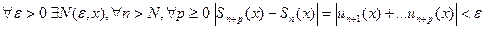Все точки, в которых ряд сходится, составляют область сходимости ряда.

Примеры. 1) Ряд сходится только в точке , во всех остальных точках ряд расходится.

2) Ряд сходится во всех точках оси, .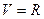

3) Ряд 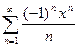сходится в области .

4) Ряд расходится во всех точках оси Æ.

Функциональный ряд 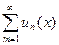называется равномерно сходящимся в области V, если

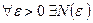, что .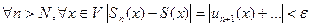

Здесь номер N зависит только от , но не от точки x, поэтому номер N выбирается сразу для всей области V. Ряд сходится с одной и той же скоростью для всех точек области V. Такая сходимость напоминает сходимость числовых рядов. Действительно, равномерно сходящиеся ряды обладают очень полезными свойствами, которые мы обсудим ниже.

Критерий Коши равномерной сходимости ряда.

Для того чтобы функциональный ряд 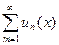равномерно сходился в области V, необходимо и достаточно, чтобы .

Дата добавления: 2014-01-11